题目内容
如图2-3-36,在四棱锥P—ABCD中,底面ABCD是∠DAB=60°,且边长为a的菱形.侧面PAD为正三角形,其所在的平面垂直于底面ABCD.
图2-3-36
(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.
思路分析:对于第(1)问,要证直线与平面垂直,已知面PAD⊥平面ABCD,只要证明BG与交线AD垂直即可;对第(2)问,由于AD∥BC,故只要证BC⊥PB;第(3)问是开放性的问题,可以选取特殊点,如取PC的中点F来讨论.
(1)解:∵在菱形ABCD中,∠DAB=60°,G为AD的中点,
∴BG⊥AD.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴BG⊥平面PAD.
(2)证明:连结PG.
∵△PAD为正三角形,G为AD的中点,
∴PG⊥AD.
由(1)知BG⊥AD,PG∩BG=G,PG![]() 平面PGB,BG
平面PGB,BG![]() 平面PGB,
平面PGB,
∴AD⊥平面PGB.
∵PB![]() 平面PGB,∴AD⊥PB.
平面PGB,∴AD⊥PB.
(3)证明:当F为PC的中点时,满足平面DEF⊥平面ABCD.
取PC的中点F,连结DE、EF、DF,
则由平面几何知识,在△PBC中,FE∥PB.
在菱形ABCD中,GB∥DE.
而FE![]() 平面DEF,DE
平面DEF,DE![]() 平面DEF,FE∩DE=E,
平面DEF,FE∩DE=E,
∴平面DEF∥平面PGB.
由(1),PG⊥平面ABCD,而PG![]() 平面PGB,
平面PGB,
∴平面PGB⊥平面ABCD.
∴平面DEF⊥平面ABCD.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,CD=2,AB=3,∠ABC=60°,将此梯形以AD所在直线为轴旋转一周,所得几何体的表面积是( )
如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,CD=2,AB=3,∠ABC=60°,将此梯形以AD所在直线为轴旋转一周,所得几何体的表面积是( )| A、46π | B、23π | C、26π | D、36π |
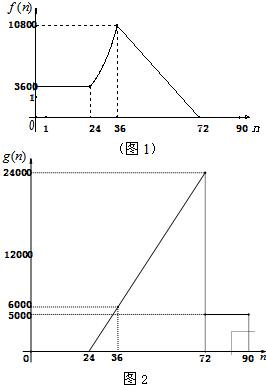 2010年上海世博会组委会为保证游客参观的顺利进行,对每天在各时间段进入园区和离开园区的人数作了一个模拟预测.为了方便起见,以10分钟为一个计算单位,上午9点10分作为第一个计算人数的时间,即n=1;9点20分作为第二个计算人数的时间,即n=2;依此类推…,把一天内从上午9点到晚上24点分成了90个计算单位.
2010年上海世博会组委会为保证游客参观的顺利进行,对每天在各时间段进入园区和离开园区的人数作了一个模拟预测.为了方便起见,以10分钟为一个计算单位,上午9点10分作为第一个计算人数的时间,即n=1;9点20分作为第二个计算人数的时间,即n=2;依此类推…,把一天内从上午9点到晚上24点分成了90个计算单位. 某企业新研制一种LED节能灯管,为了测试其使用寿命,从中随机抽取50支灯管作为测试样本,分别在使用了12个月、24个月、36个月时进行3次测试,得到未损坏的灯管支数如下表:
某企业新研制一种LED节能灯管,为了测试其使用寿命,从中随机抽取50支灯管作为测试样本,分别在使用了12个月、24个月、36个月时进行3次测试,得到未损坏的灯管支数如下表: