题目内容
已知点A、B、C都在球面上 且球心O到平面ABC的距离等于球的半径的
,而AB=2,AC=2
,BC=2
,设三棱椎O-ABC的体积为V1,球的体积为V2,求
.
| 1 |
| 2 |
| 2 |
| 3 |
| V1 |
| V2 |
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:求出三角形ABC的外心,利用球心到△ABC所在平面的距离为球半径的一半,求出球的半径,即可求出三棱椎O-ABC的体积为V1,球的体积为V2,从而求
.
| V1 |
| V2 |
解答:
解:由题意AB=2,AC=2
,BC=2
,∵AB2+AC2=BC2,可知三角形是直角三角形,
三角形的外心是BC的中点,球心到截面的距离就是球心与三角形外心的距离,
设球的半径为R,球心到△ABC所在平面的距离为球半径的一半,
所以R2=(
R)2+32,
解得R2=36,
∴V2=144π,V1=
×
×2×2
×3=2
,
∴
=
.
| 2 |
| 3 |
三角形的外心是BC的中点,球心到截面的距离就是球心与三角形外心的距离,
设球的半径为R,球心到△ABC所在平面的距离为球半径的一半,
所以R2=(
| 1 |
| 2 |
解得R2=36,
∴V2=144π,V1=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
∴
| V1 |
| V2 |
| ||
| 72 |
点评:本题是中档题,考查球的内接多面体,找出球的半径满足的条件是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
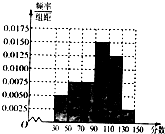 从某校高一期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图,如图所示.根据频率分布直方图,估计该次数学考试的平均分为( )
从某校高一期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图,如图所示.根据频率分布直方图,估计该次数学考试的平均分为( )| A、46 | B、82 | C、92 | D、102 |
 如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,求⊙O的半径.
如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,求⊙O的半径.