题目内容
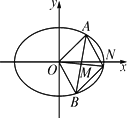
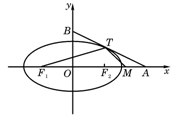
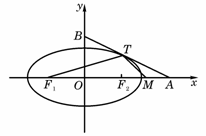
如图,椭圆![]() =1(a>b>0)与过点A(2,0)、B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
=1(a>b>0)与过点A(2,0)、B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=![]() .
.

(1)求椭圆方程;
(2)设F1、F2分别为椭圆的左、右焦点,M为线段AF2的中点,求证:∠ATM=∠AF1T.
答案:
解析:
解析:
|
解析:(1)过点A、B的直线方程为 因为由题意得 即(b2+ 所以Δ=a2b2(a2+4b2-4)=0(ab≠0), 故a2+4b2-4=0. 又因为e= 所以a2=4b2,从而得a2=2,b2= 故所求的椭圆方程为 (2)由(1)得c= 从而M( 由 所以T(1, 因为tan∠AF1T= 又tan∠TAM= tan∠ATM= 因此∠ATM=∠AF1T. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
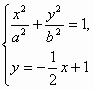 有惟一解,
有惟一解,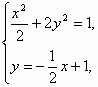 解得x1=x2=1,
解得x1=x2=1, ,
,