题目内容
如图,E是圆O内两弦AB和CD的交点F是AD延长线上一点,FG与圆O相切于点G,且EF=FG,求证:
(1)△EFD~△AFE;
(2)EF∥BC.
(1)△EFD~△AFE;
(2)EF∥BC.

证明:(1)∵FG与圆O相切于点G,
∴FG2=FD FA,
FA,
∵EF=FG,EF2=FD FA,∴
FA,∴  =
=  ,
,
∵∠EFD=∠AFE,∴△EFD∽△AFE.
(2)由(1),有∠FED=∠FAE,
∵∠FAE和∠BCD都是 上的圆周角,
上的圆周角,
∴∠FED=∠BCD,
∴EF∥BC.
∴FG2=FD
 FA,
FA, ∵EF=FG,EF2=FD
 FA,∴
FA,∴  =
=  ,
,∵∠EFD=∠AFE,∴△EFD∽△AFE.
(2)由(1),有∠FED=∠FAE,
∵∠FAE和∠BCD都是
 上的圆周角,
上的圆周角,∴∠FED=∠BCD,
∴EF∥BC.

练习册系列答案
相关题目
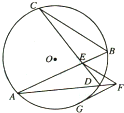 如图,E是圆O内两弦AB和CD的交点F是AD延长线上一点,FG与圆O相切于点G,且EF=FG,求证:
如图,E是圆O内两弦AB和CD的交点F是AD延长线上一点,FG与圆O相切于点G,且EF=FG,求证: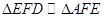 ;
;
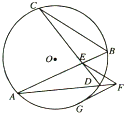 如图,E是圆O内两弦AB和CD的交点F是AD延长线上一点,FG与圆O相切于点G,且EF=FG,求证:
如图,E是圆O内两弦AB和CD的交点F是AD延长线上一点,FG与圆O相切于点G,且EF=FG,求证: