题目内容
点P是方程
-
=6所表示的曲线上的点,若点P的纵坐标是4,则其横坐标为 .
| (x-5)2+y2 |
| (x+5)2+y2 |
分析:根据两点间的距离公式与双曲线的定义,可得点P的轨迹是以F1(-5,0)、F2(5,0)为焦点的双曲线的左支.由题中数据求出双曲线的方程,再将y=4代入解出x的值,即可得出点P的横坐标.
解答:解:设点P(x,y),F1(-5,0),F2(5,0),
可得|PF1|=
,|PF2|=
.
∵
-
=6,
∴点P满足|PF2|-|PF1|=6,可得点P的轨迹是以F1、F2为焦点的双曲线的左支.
又∵c=5,2a=6,得a=3,∴b2=c2-a2=25-9=16,
因此该双曲线的方程为
-
=1(x<0),
若点P的纵坐标是4,则将y=4代入双曲线方程,得
-
=1,解得x=-3
(正值舍去).
∴点P的横坐标为-3
.
故答案为:-3
可得|PF1|=
| (x+5)2+y2 |
| (x-5)2+y2 |
∵
| (x-5)2+y2 |
| (x+5)2+y2 |
∴点P满足|PF2|-|PF1|=6,可得点P的轨迹是以F1、F2为焦点的双曲线的左支.
又∵c=5,2a=6,得a=3,∴b2=c2-a2=25-9=16,
因此该双曲线的方程为
| x2 |
| 9 |
| y2 |
| 16 |
若点P的纵坐标是4,则将y=4代入双曲线方程,得
| x2 |
| 9 |
| 42 |
| 16 |
| 2 |
∴点P的横坐标为-3
| 2 |
故答案为:-3
| 2 |
点评:本题给出动点P满足的等式,求当P的纵坐标为4时P的横坐标.着重考查了双曲线的定义与标准方程等知识,属于基础题.

练习册系列答案
相关题目
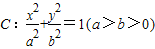 的左右焦点,A(0,b),连接AF1并延长交椭圆C于B点,若
的左右焦点,A(0,b),连接AF1并延长交椭圆C于B点,若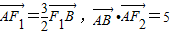 ,
,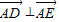 ?若存在,求出点P的坐标,若不存在,请说明理由.
?若存在,求出点P的坐标,若不存在,请说明理由.