题目内容
已知F1、F2是椭圆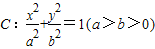 的左右焦点,A(0,b),连接AF1并延长交椭圆C于B点,若
的左右焦点,A(0,b),连接AF1并延长交椭圆C于B点,若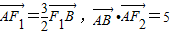 ,
,(1)求椭圆C的方程;
(2)设P是直线x=5上的一点,直线PF2交椭圆C于D、E两点,是否存在这样的点P,使得
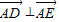 ?若存在,求出点P的坐标,若不存在,请说明理由.
?若存在,求出点P的坐标,若不存在,请说明理由.
【答案】分析:(1)设出B点的坐标,写出所用向量的坐标,利用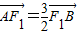 列式求出B的坐标(用含有b,c的代数式表示),然后分别用B在椭圆上和
列式求出B的坐标(用含有b,c的代数式表示),然后分别用B在椭圆上和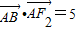 列式联立方程组求解a,b,c,则椭圆方程可求;
列式联立方程组求解a,b,c,则椭圆方程可求;
(2)假设存在点P,由题意设出DE所在直线方程,和椭圆方程联立后化为关于x的一元二次方程,利用根与系数关系求出D,E两点的横坐标的和与积,把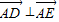 转化为坐标运算,代入根与系数关系后求出k的值,
转化为坐标运算,代入根与系数关系后求出k的值,
求出直线方程后验证即可得到答案.
解答:解:(1)设B(x,y),又F1(-c,0),A(0,b),F2(c,0).
∴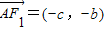 ,
,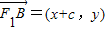 ,
,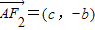 .
.
∵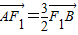 ,∴
,∴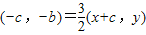 ,
,
∴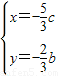 ,即
,即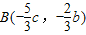 ,
,
则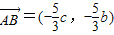 .
.
又点B在椭圆上,∴a2=5c2,
又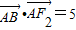 ,即
,即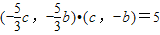 ,
,
∴b2-c2=3,又∵a2=b2+c2,∴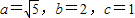 .
.
∴椭圆C的方程为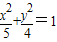 ;
;
(2)假设存在点P,由题意知直线DE的斜率一定存在,设为k,
则DE的方程为y=k(x-1),又设D(x1,y1),E(x2,y2),
由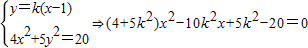
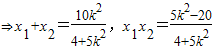 .
.
∵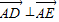 ,∴
,∴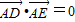 ,
,
∴x1x2+(y1-2)(y2-2)=0,x1x2+(kx1-k-2)(kx2-k-2)=0.
即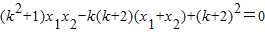 ,代入得
,代入得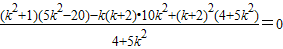
化简,得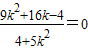 ,解得k=-2或
,解得k=-2或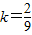 .
.
当k=-2时,直线DE的方程为y=-2x+2,由于直线DE过点A,不合题意.
当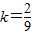 时,直线DE的方程为
时,直线DE的方程为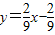 ,与x=5联立,求得点
,与x=5联立,求得点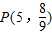 .
.
因此存在点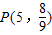 满足题意.
满足题意.
点评:本题主要考查了直线与圆锥曲线的位置关系的应用,直线与曲线联立,利用方程的根与系数的关系是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力,是难题.
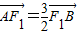 列式求出B的坐标(用含有b,c的代数式表示),然后分别用B在椭圆上和
列式求出B的坐标(用含有b,c的代数式表示),然后分别用B在椭圆上和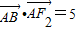 列式联立方程组求解a,b,c,则椭圆方程可求;
列式联立方程组求解a,b,c,则椭圆方程可求;(2)假设存在点P,由题意设出DE所在直线方程,和椭圆方程联立后化为关于x的一元二次方程,利用根与系数关系求出D,E两点的横坐标的和与积,把
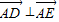 转化为坐标运算,代入根与系数关系后求出k的值,
转化为坐标运算,代入根与系数关系后求出k的值,求出直线方程后验证即可得到答案.
解答:解:(1)设B(x,y),又F1(-c,0),A(0,b),F2(c,0).
∴
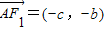 ,
,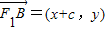 ,
,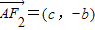 .
.∵
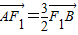 ,∴
,∴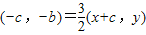 ,
,∴
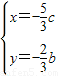 ,即
,即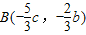 ,
,则
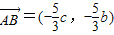 .
.又点B在椭圆上,∴a2=5c2,
又
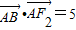 ,即
,即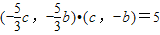 ,
,∴b2-c2=3,又∵a2=b2+c2,∴
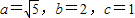 .
.∴椭圆C的方程为
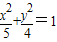 ;
;(2)假设存在点P,由题意知直线DE的斜率一定存在,设为k,
则DE的方程为y=k(x-1),又设D(x1,y1),E(x2,y2),
由
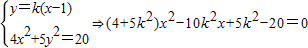
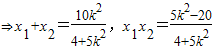 .
.∵
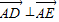 ,∴
,∴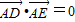 ,
,∴x1x2+(y1-2)(y2-2)=0,x1x2+(kx1-k-2)(kx2-k-2)=0.
即
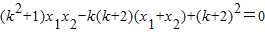 ,代入得
,代入得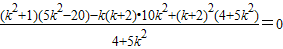
化简,得
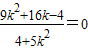 ,解得k=-2或
,解得k=-2或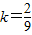 .
.当k=-2时,直线DE的方程为y=-2x+2,由于直线DE过点A,不合题意.
当
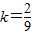 时,直线DE的方程为
时,直线DE的方程为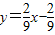 ,与x=5联立,求得点
,与x=5联立,求得点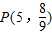 .
.因此存在点
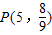 满足题意.
满足题意.点评:本题主要考查了直线与圆锥曲线的位置关系的应用,直线与曲线联立,利用方程的根与系数的关系是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力,是难题.

练习册系列答案
相关题目