题目内容
规定A =x(x-1)…(x-m+1),其中x∈R,m为正整数,且
=x(x-1)…(x-m+1),其中x∈R,m为正整数,且 =1,这是排列数A
=1,这是排列数A (n,m是正整数,n≤m)的一种推广.
(n,m是正整数,n≤m)的一种推广.(Ⅰ) 求A
 的值;
的值;(Ⅱ)排列数的两个性质:①A
 =nA
=nA ,②A
,②A +mA
+mA =A
=A (其中m,n是正整数).是否都能推广到A
(其中m,n是正整数).是否都能推广到A (x∈R,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(x∈R,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;(Ⅲ)已知函数f(x)=A
 -4lnx-m,试讨论函数f(x)的零点个数.
-4lnx-m,试讨论函数f(x)的零点个数.
【答案】分析:(Ⅰ)直接代入定义求解;
(Ⅱ)利用新定义,结合排列数的两个性质即可证明推广的结论;
(Ⅲ)由新定义展开函数f(x),求导后得其导函数的零点,得其在各区间段内的单调性,然后对m进行讨论得其零点个数.
解答:解:(Ⅰ)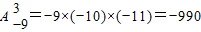 ;
;
(Ⅱ)性质①、②均可推广,推广的形式分别是①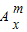 =
=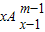 ,②
,②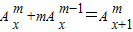 (x∈R,m∈N*)
(x∈R,m∈N*)
证明:①当m=1时,左边=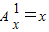 ,右边=
,右边=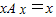 ,等式成立;
,等式成立;
当m≥2时,
左边=x(x-1)…(x-m+1)=x{(x-1)(x-2)…[(x-1)-(m-1)+1]}=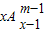 .
.
因此,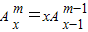 (x∈R,m∈N*)成立.
(x∈R,m∈N*)成立.
②当m=1时,左边=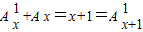 =右边,等式成立;
=右边,等式成立;
当m≥2时,左边x(x-1)…(x-m+1)+mx(x-1)…(x-m+2)
=x(x-1)…(x-m+2)(x-m+1+m)
=(x+1)x(x-1)…(x-m+2)
=(x+1)x(x-1)…[(x+1)-m=1]
=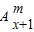 =右边
=右边
因此,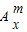 +m
+m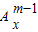 =
=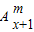 (x∈R,m∈N*)成立.
(x∈R,m∈N*)成立.
(Ⅲ)f(x)=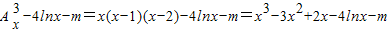
设函数g(x)=x3-3x2+2x-4lnx,
函数f(x)零点的个数等价于函数g(x)与y=m公共点的个数.
f(x)的定义域为(0,+∞)
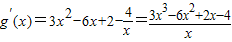 =
=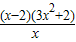 .
.
令g′(x)=0,得x=2
∴当m<-4ln2时,函数g(x)与y=m没有公共点,即函数f(x)不存在零点,
当m=-4ln2时,函数g(x)与y=m有一个公共点,即函数f(x)有且只有一个零点,
当m>-4ln2时,函数g(x)与y=m有两个公共点,即函数f(x)有且只有两个零点.
点评:本题考查了排列及排列数公式,考查了利用导函数判断原函数的单调性,考查了分类讨论的数学思想方法,解答的关键是对新定义的理解与运用,是中档题.
(Ⅱ)利用新定义,结合排列数的两个性质即可证明推广的结论;
(Ⅲ)由新定义展开函数f(x),求导后得其导函数的零点,得其在各区间段内的单调性,然后对m进行讨论得其零点个数.
解答:解:(Ⅰ)
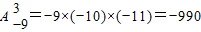 ;
;(Ⅱ)性质①、②均可推广,推广的形式分别是①
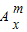 =
=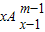 ,②
,②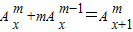 (x∈R,m∈N*)
(x∈R,m∈N*)证明:①当m=1时,左边=
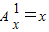 ,右边=
,右边=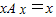 ,等式成立;
,等式成立;当m≥2时,
左边=x(x-1)…(x-m+1)=x{(x-1)(x-2)…[(x-1)-(m-1)+1]}=
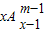 .
.因此,
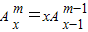 (x∈R,m∈N*)成立.
(x∈R,m∈N*)成立.②当m=1时,左边=
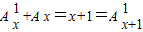 =右边,等式成立;
=右边,等式成立;当m≥2时,左边x(x-1)…(x-m+1)+mx(x-1)…(x-m+2)
=x(x-1)…(x-m+2)(x-m+1+m)
=(x+1)x(x-1)…(x-m+2)
=(x+1)x(x-1)…[(x+1)-m=1]
=
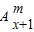 =右边
=右边因此,
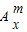 +m
+m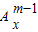 =
=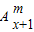 (x∈R,m∈N*)成立.
(x∈R,m∈N*)成立.(Ⅲ)f(x)=
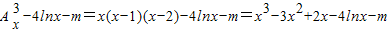
设函数g(x)=x3-3x2+2x-4lnx,
函数f(x)零点的个数等价于函数g(x)与y=m公共点的个数.
f(x)的定义域为(0,+∞)
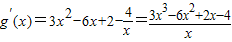 =
=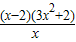 .
.令g′(x)=0,得x=2
| x | (0,2) | 2 | (2,+∞) |
| g′(x) | - | + | |
| g(x) | 减 | -4ln2 | 增 |
当m=-4ln2时,函数g(x)与y=m有一个公共点,即函数f(x)有且只有一个零点,
当m>-4ln2时,函数g(x)与y=m有两个公共点,即函数f(x)有且只有两个零点.
点评:本题考查了排列及排列数公式,考查了利用导函数判断原函数的单调性,考查了分类讨论的数学思想方法,解答的关键是对新定义的理解与运用,是中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 =x(x+1)(x+2)…(x+n-1),例如:
=x(x+1)(x+2)…(x+n-1),例如: (-3)•(-2)•(-1)=-6,则函数f(x)=x•
(-3)•(-2)•(-1)=-6,则函数f(x)=x• ( )
( )