题目内容
17.已知x为三角形中的最小角,则函数$y=sinx+\sqrt{3}cosx+1$的值域为[$\sqrt{3}+1$,3].分析 由x为三角形中的最小内角,可得0<x≤$\frac{π}{3}$,而$y=sinx+\sqrt{3}cosx+1$=2sin(x+$\frac{π}{3}$)+1,结合已知所求的x的范围可求y的范围.
解答 解:x为三角形中的最小内角,由三角形的内角和定理可知:
0<x≤$\frac{π}{3}$,
$y=sinx+\sqrt{3}cosx+1$=2sin(x+$\frac{π}{3}$)+1,
由0<x≤$\frac{π}{3}$,即$\frac{π}{3}$<x+$\frac{π}{3}$≤$\frac{2π}{3}$,
∴$\frac{\sqrt{3}}{2}$≤sin(x+$\frac{π}{3}$)≤1,
$\sqrt{3}$+1≤2sin(x+$\frac{π}{3}$)+1≤3,
函数$y=sinx+\sqrt{3}cosx+1$的值域[$\sqrt{3}+1$,3]
故答案为:[$\sqrt{3}+1$,3].
点评 本题主要考查了辅助角公式的应用,考查三角形的内角和定理的应用,正弦函数的图象的性质,属于中档题.

练习册系列答案
相关题目
7.已知函数y=f(x)在定义域(-1,1)上是减函数,且f(2a-1)<f(1-a),则实数a的取值范围是( )
| A. | ($\frac{2}{3},+∞$) | B. | ($\frac{2}{3},1)$ | C. | (0,2) | D. | (0,+∞) |
5.幂函数f(x)=(m2-m-1)x5m+3在(0,+∞)上是增函数,则m=( )
| A. | 2 | B. | -1 | C. | 4 | D. | 2或-1 |
12.已知函数f(x)=$\left\{\begin{array}{l}{f(x-4),x>2}\\{{e}^{x},-2≤x≤2}\\{f(-x),x<-2}\end{array}$,则f(-2017)=( )
| A. | 1 | B. | e | C. | $\frac{1}{e}$ | D. | e2 |
2.已知两定点A(-1,0)和B(1,0),动点P(x,y)在直线l:y=x+3上移动,椭圆C以A,B为焦点且经过点P,则椭圆C的离心率的最大值为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{10}}{5}$ |
6.设函数f(x)=${e^x}({{x^3}+\frac{3}{2}{x^2}-6x+2})-2a{e^x}$-x,若不等式f(x)≤0在[-2,+∞)上有解,则实数a的最小值为( )
| A. | $-\frac{3}{2}-\frac{1}{e}$ | B. | $-\frac{3}{2}-\frac{2}{e}$ | C. | $-\frac{3}{4}-\frac{1}{2e}$ | D. | $-1-\frac{1}{e}$ |
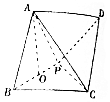 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且AB=$\sqrt{2}$,∠ABC=60°,点A在平面PBC上的射影为PB的中点O,PB⊥AC.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且AB=$\sqrt{2}$,∠ABC=60°,点A在平面PBC上的射影为PB的中点O,PB⊥AC.