题目内容
已知:平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足.(1)求证:PA⊥平面ABC;
(2)当E为△PBC的垂心时,求证:△ABC是直角三角形.
解析:已知条件“平面PAB⊥平面ABC,…”,使我们想到面面垂直的性质定理,便有如下证法.
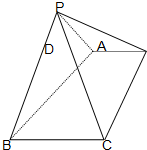
证明:如图,(1)在平面ABC内取一点D,作DF⊥AC于F,平面PAC⊥平面ABC,且交线为AC,

∴DF⊥平面PAC,PA![]() 平面PAC.
平面PAC.
∴DF⊥AP,作DG⊥AB于G,同理可证DG⊥AP,
又DG,DF都是在平面ABC内,
∴PA⊥平面ABC.
(2)作BE交PC于H,
∵E是△PBC的垂心,
∴PC⊥BE.
又AE是平面PBC的垂线,
∴PC⊥AB.
又∵PA⊥平面ABC,
∴PA⊥AB.
∴AB⊥平面PAC.
∴AB⊥AC,即△ABC是直角三角形.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目

 如图:已知四棱锥P-ABCD的底面为直角梯形,AD∥BC,∠BCD=90,PA=PB,PC=PD.
如图:已知四棱锥P-ABCD的底面为直角梯形,AD∥BC,∠BCD=90,PA=PB,PC=PD. (2013•宁波二模)如图,已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP=
(2013•宁波二模)如图,已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP= (2012•莆田模拟)如图,在三棱锥P-ABC中,△PAC,△ABC分别是以A、B为直角顶点的等腰直角三角形,AB=1.
(2012•莆田模拟)如图,在三棱锥P-ABC中,△PAC,△ABC分别是以A、B为直角顶点的等腰直角三角形,AB=1.