题目内容
 (2013•宁波二模)如图,已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP=
(2013•宁波二模)如图,已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP=| 2 |
(Ⅰ)求证:平面PAB⊥平面ABCD;
(Ⅱ)求二面角A-PC-D的平面角的余弦值.
分析:(I)取AB中点E,连PE、CE,由等腰三角形的性质可得PE⊥AB.再利用勾股定理的逆定理可得PE⊥CE.利用线面垂直的判定定理可得PE⊥平面ABCD.再利用面面垂直的判定定理即可证明.
(II)建立如图所示的空间直角坐标系.利用两个平面的法向量的夹角即可得到二面角.
(II)建立如图所示的空间直角坐标系.利用两个平面的法向量的夹角即可得到二面角.
解答:(Ⅰ)证明:如图1所示,取AB中点E,连PE、CE.
则PE是等腰△PAB的底边上的中线,∴PE⊥AB.
∵PE=1,CE=
,PC=2,即PE2+CE2=PC2.
由勾股定理的逆定理可得,PE⊥CE.
又∵AB?平面ABCD,CE?平面ABCD,且AB∩CE=E,
∴PE⊥平面ABCD.
而PE?平面PAB,
∴平面PAB⊥平面ABCD.
(Ⅱ)以AB中点E为坐标原点,EC所在直线为x轴,EB所在直线为y轴,EP所在直线为z轴,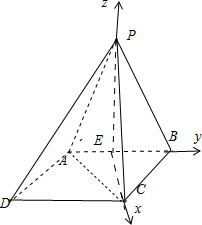
建立如图所示的空间直角坐标系.
则A(0,-1,0),C(
,0,0),D(
,-2,0),P(0,0,1),
=(
,1,0),
=(
,0,-1),
=(0,2,0).
设
=(x1,y1,z1)是平面PAC的一个法向量,
则
,即
.
取x1=1,可得y1=-
, z1=
,
=(1,-
,
).
设
=(x2,y2,z2)是平面PCD的一个法向量,
则
,即
.
取x2=1,可得y2=0, z2=
,
=(1,0,
).
故cos<
,
>=
=
,
即二面角A-PC-D的平面角的余弦值是
.
则PE是等腰△PAB的底边上的中线,∴PE⊥AB.
∵PE=1,CE=
| 3 |
由勾股定理的逆定理可得,PE⊥CE.
又∵AB?平面ABCD,CE?平面ABCD,且AB∩CE=E,
∴PE⊥平面ABCD.
而PE?平面PAB,
∴平面PAB⊥平面ABCD.
(Ⅱ)以AB中点E为坐标原点,EC所在直线为x轴,EB所在直线为y轴,EP所在直线为z轴,

建立如图所示的空间直角坐标系.
则A(0,-1,0),C(
| 3 |
| 3 |
| AC |
| 3 |
| PC |
| 3 |
| DC |
设
| n1 |
则
|
|
取x1=1,可得y1=-
| 3 |
| 3 |
| n1 |
| 3 |
| 3 |
设
| n2 |
则
|
|
取x2=1,可得y2=0, z2=
| 3 |
| n2 |
| 3 |
故cos<
| n1 |
| n2 |
| ||||
|
|
| 2 |
| 7 |
| 7 |
即二面角A-PC-D的平面角的余弦值是
| 2 |
| 7 |
| 7 |
点评:熟练掌握等腰三角形的性质、勾股定理的逆定理、线面垂直的判定定理、面面垂直、通过建立空间直角坐标系并利用两个平面的法向量的夹角得到二面角的方法等是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 (2013•宁波二模)如图是某学校抽取的n个学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第3个小组的频数为18,则的值n是
(2013•宁波二模)如图是某学校抽取的n个学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第3个小组的频数为18,则的值n是