题目内容
设函数f(x)=logax(a>0且a≠1),若f(x1x2x3…x2011)=8,则f( )+f(
)+f( )+…+f(
)+…+f(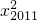 )的值为
)的值为
- A.4
- B.8
- C.16
- D.2loga8
C
分析:把f(x1x2x3…x2011)=8代入函数解析式得到loga(x1x2x3…x2011)=8,把f( )+f(
)+f( )+…+f(
)+…+f(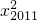 )代入函数解析式后利用对数的和等于乘积的对数化简,然后把loga(x1x2x3…x2011)=8代入化简后的式子即可求得答案.
)代入函数解析式后利用对数的和等于乘积的对数化简,然后把loga(x1x2x3…x2011)=8代入化简后的式子即可求得答案.
解答:由f(x)=logax,则f(x1x2x3…x2011)=loga(x1x2x3…x2011)=8,
则f( )+f(
)+f( )+…+f(
)+…+f(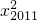 )
)
=
=
=
=2loga(x1x2…x2011)
=2×8=16.
故选C.
点评:本题考查了对数的运算性质,考查了整体运算思想,是基础的计算题.
分析:把f(x1x2x3…x2011)=8代入函数解析式得到loga(x1x2x3…x2011)=8,把f(
 )+f(
)+f( )+…+f(
)+…+f(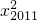 )代入函数解析式后利用对数的和等于乘积的对数化简,然后把loga(x1x2x3…x2011)=8代入化简后的式子即可求得答案.
)代入函数解析式后利用对数的和等于乘积的对数化简,然后把loga(x1x2x3…x2011)=8代入化简后的式子即可求得答案.解答:由f(x)=logax,则f(x1x2x3…x2011)=loga(x1x2x3…x2011)=8,
则f(
 )+f(
)+f( )+…+f(
)+…+f(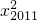 )
)=

=

=

=2loga(x1x2…x2011)
=2×8=16.
故选C.
点评:本题考查了对数的运算性质,考查了整体运算思想,是基础的计算题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目