题目内容
求证:当x＞0时,ln(1+
)＞
.
分析：要证ln(1+)＞,
只需证ln(1+
)-
＞0,
即证x＞0时,f(x)=ln(1+
)-
的值为正.
证明：令F(x)=ln(1+
)-
(x＞0),
∵F′(x)=
(-
)+
=
-
=
＜0(x＞0),
∴F(x)在(0，+∞)上是减函数.
又
F(x)=
［ln(1+
)-
］=0,
∴F(x)＞0,即ln(1+
)-
＞0.
∴ln(1+
)＞
.
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
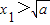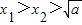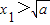）处的切线为l，l与x轴交于点A（x2，0），求证：
．
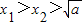）处的切线为l，l与x轴交于点A（x2，0），求证：
．
）处的切线为l，l与x轴交于点A（x2，0），求证：
．