题目内容
如图直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=(Ⅰ)求证:CD⊥平面BDM;
(Ⅱ)求平面B1BD与平面CBD所成锐二面角的大小.
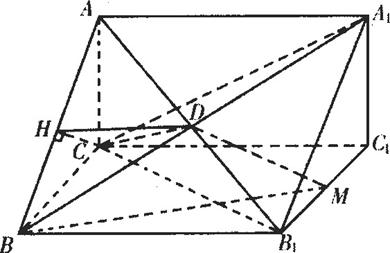
(Ⅰ)证明:连CA1由直三棱柱ABC-A1B1C1得A1A⊥AC
Rt△AA1C中可得CA1=BC=![]()
又D为BA1中点 ∴CD⊥BA1(2分)
连CB1,在Rt△CBB1和Rt△BB1M中,![]()

∴Rt△CBB1∽Rt△BB1M ∴∠B1CB=∠MBB1
又∵CB⊥BB1 ∴CB1⊥BM
又∵AC⊥BC ∴AC⊥面CBB1C1
∴AC⊥BM ∴BM⊥面ACB1 ∴BM⊥CD
又∵BA1∩BM=B ∴CD⊥面BDM
(Ⅱ)过C作CH⊥AB垂足H,连DH
由直三棱柱ABC-A1B1C1得面ABC⊥面ABB1A1
∴CH⊥面ABB1A1
又由(Ⅰ)知CD⊥BD ∴据三垂线定理得DH⊥BD
∴∠HDC是平面B1BD与平面CBD所成锐二面角的平面角
Rt△ACB中可求得CH=![]() Rt△BCD中可求得CD=1
Rt△BCD中可求得CD=1
Rt△HDC中,sin∠HDC=![]()
∴平面B1BD与平面CBD所成锐二面角的大小为arcsin![]()

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
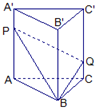 如图直三棱柱ABC-A1B1C1的体积为V,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B-APQC的体积为( )
如图直三棱柱ABC-A1B1C1的体积为V,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B-APQC的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
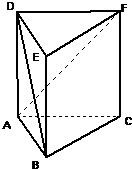 16、如图直三棱柱ABC-DEF中,∠CAB是直角,AB=AC=CF,则异面直线DB与AF所成角的度数为
16、如图直三棱柱ABC-DEF中,∠CAB是直角,AB=AC=CF,则异面直线DB与AF所成角的度数为
 (2008•徐汇区二模)如图直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,∠ABC=90°,AC=2,D是AA1的中点
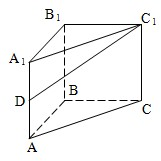
(2008•徐汇区二模)如图直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,∠ABC=90°,AC=2,D是AA1的中点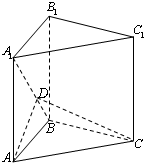 (2012•咸阳三模)如图直三棱柱ABC-A1B1C1中,AC=CC1=2,AB=BC,D是BA1上一点,且AD⊥平面A1BC.
(2012•咸阳三模)如图直三棱柱ABC-A1B1C1中,AC=CC1=2,AB=BC,D是BA1上一点,且AD⊥平面A1BC. (2012•咸阳三模)如图直三棱柱ABC-A1B1C1中,AC=CC1=2,AB=BC,D是BA1上一点,且AD⊥平面A1BC.
(2012•咸阳三模)如图直三棱柱ABC-A1B1C1中,AC=CC1=2,AB=BC,D是BA1上一点,且AD⊥平面A1BC.