题目内容
已知数列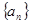 的首项为
的首项为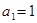 ,其前
,其前 项和为
项和为 ,且对任意正整数
,且对任意正整数 有:
有: 、
、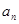 、
、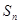 成等差数列.
成等差数列.
(1)求证:数列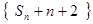 成等比数列;
成等比数列;
(2)求数列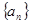 的通项公式.
的通项公式.
【答案】
(1) ,当
,当 时,
时, ,所以
,所以 ,
,
即 ,又
,又 ,所以
,所以 成以4为首项、2为公比的等比数列(2)
成以4为首项、2为公比的等比数列(2)
【解析】
试题分析:⑴因对任意 有
有 成等差数列,所以
成等差数列,所以 2分
2分
又当 时,
时, ,所以
,所以 ,
4分
,
4分
即 ,又
,又 ,
,
所以 成以4为首项、2为公比的等比数列
6分
成以4为首项、2为公比的等比数列
6分
⑵由⑴得 ,所以
,所以
当 时,
时,
又 满足此式,所以
满足此式,所以 12分
12分
考点:等比数列证明及数列求通项
点评:证明数列是等比数列一般采用定义,即相邻两项的比值是常数,本题求通项用到了公式

练习册系列答案
相关题目
已知数列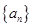 的首项
的首项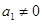 ,其前
,其前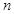 项的和为
项的和为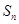 ,且
,且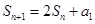 ,则
,则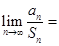
| A.0 | B.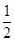 | C.1 | D.2 |
 的首项
的首项 ,其前n项和为
,其前n项和为 .若
.若 ,则
,则 .
.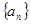 的首项为
的首项为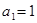 ,其前
,其前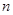 项和为
项和为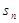 ,且对任意正整数
,且对任意正整数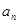 、
、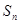 成等差数列.
成等差数列.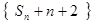 成等比数列;
成等比数列;  的首项
的首项 ,其前
,其前 项的和为
项的和为 ,且
,且 ,则
,则
 (C)
1 (D)2
(C)
1 (D)2