题目内容
(本小题12分)已知数列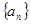 的首项为
的首项为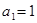 ,其前
,其前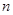 项和为
项和为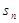 ,且对任意正整数
,且对任意正整数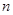 有:
有: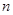 、
、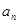 、
、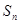 成等差数列.
成等差数列.
(1)求证:数列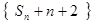 成等比数列;
成等比数列;
(2)求数列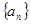 的通项公式.
的通项公式.
【答案】
(1)根据等比数列的定义,构造整体的相邻两项的比值,然后结合定义加以证明。
(2)
【解析】
试题分析:解:(1)证明:




即

(2)由(1)知 是以
是以 为首项,2为公比的等比数列
为首项,2为公比的等比数列
 , 又
, 又

考点:等比数列,数列递推式
点评:本题考查等比数列的证明,考查数列递推式,考查数列的通项,求得数列是等比数列是关键.

练习册系列答案
相关题目
 中,
中, 。
。 中,
中, ,求数列
,求数列 项和
项和 .
. 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程 ;
; 过
过 且与圆C相切,求直线
且与圆C相切,求直线 ,使直线
,使直线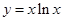
 处的切线方程。
处的切线方程。