题目内容
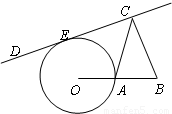
选做题 (几何证明选讲)如图,AB是⊙O的直径,C、F为⊙O上的点,CA是∠BAF的角平分线,过点C作CD⊥AF交AF的延长线于D点,作CM⊥AB,垂足为点M.
(1)求证:DC是⊙O的切线;
(2)求证:AM·MB=DF·DA.
证明:(1)连结OC,∴∠OAC=∠OCA.又∵CA是∠BAF的角平分线,∴∠OAC=∠FAC.
∴∠FAC=∠OCA.∴OC∥AD.∵CD⊥AD,∴CD⊥OC,即CD是⊙O的切线.
(2)连结BC,则在Rt△ACB中,CM2=AM·MB.∵CD是⊙O的切线,
∴CD2=DF·DA.又Rt△AMC≌Rt△ADC,∴CM=CD.∴AM·MB=DF·DA.
练习册系列答案
名校课堂系列答案
相关题目
选做题在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．
（2012•宝鸡模拟）（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
∠OAC．
，向量
．求向量
，使得A2
=
．
，焦距为2，求实数a的值．
（a，b．c为实数）的最小值为m，若a-b+2c=3，求m的最小值．