Question

选做题在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．
A选修4-1：几何证明选讲
如图，延长⊙O的半径OA到B，使OA=AB，DE是圆的一条切线，E是切点，过点B作DE的垂线，垂足为点C．
求证：∠ACB=∠OAC．
B选修4-2：矩阵与变换
已知矩阵A=，向量．求向量，使得A²=．
C选修4-3：坐标系与参数方程
已知椭圆C的极坐标方程为ρ²=，焦距为2，求实数a的值．
D选修4-4：不等式选讲
已知函数f（x）=（x-a）²+（x-b）²+（x-c）²+（a，b．c为实数）的最小值为m，若a-b+2c=3，求m的最小值．

Answer 1

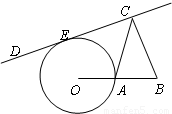
【答案】分析：A连接OE，AE，并过点A作AF⊥DE于点F，由DE是切线，知OE⊥DC，由BC⊥DE，知OE∥AF∥BC，由此能够推导出∠ACB=∠OAC．
B由A=，知A²==，设=，则，由此能求出向量，使得A²=．
C由椭圆C的极坐标方程得到，由此能求出a．
D由f（x）=（x-a）²+（x-b）²+（x-c）²+=3（x-）²+a²+b²+c²．知x=时，f（x）取最小值a²+b²+c²，即m=a²+b²+c²，由此利用柯西不等式能求出m的最小值．
解答：解：A证明：连接OE，AE，并过点A作AF⊥DE于点F，
∵DE是圆的一条切线，E是切点，∴OE⊥DC，
又∵BC⊥DE，∴OE∥AF∥BC，
∴∠CAF=∠ACB，∠FAE=∠AEO，
∵OA=OE，∴∠AEO=∠EAO，∴∠EAO=∠FAE，
又∵点A是OB的中点，∴点F是EC的中点，
∴AE=AC，
∴∠CAF=∠FAE，
∴∠EAO=∠FAE=∠CAF，
∴∠ACB=∠OAC．
B∵A=，∴A²==，
设=，则，
∴=，∴，
解得x=-1，y=2，∴．
C∵椭圆C的极坐标方程为ρ²=，焦距为2，
∴，
由=1，得a=12．
D∵f（x）=（x-a）²+（x-b）²+（x-c）²+
=3x²-2（a+b+c）x+a²+b²+c²+
=3（x-）²+a²+b²+c²．
∴x=时，f（x）取最小值a²+b²+c²，即m=a²+b²+c²，
∵a-b+2c=3，由柯西不等式得
[1²+（-1）²+2²]•（a²+b²+c²）≥（a-b+2c）²=9，
∴m=a²+b²+c²，
当且仅当，即a=，b=-，c=时等号成立，
∴m的最小值为．
点评：本题考查与圆有关的比例线段的应用，考查矩阵与变换的应用，考查椭圆的极坐标方程，考查柯西不等式的应用，解题时要认真审题，注意等价转化思想的合理运用．