题目内容
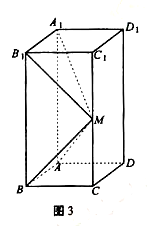
(本题满分15分)在直角梯形A1A2A3D中,A1A2⊥A1D,A1A2⊥A2A3,且B,C分别是边A1A2,A2A3上的一点,沿线段 BC,CD,DB分别将△BCA2,△CDA3,△DBA1翻折上去恰好使A1,A2,A3重合于一点A。
BC,CD,DB分别将△BCA2,△CDA3,△DBA1翻折上去恰好使A1,A2,A3重合于一点A。
(Ⅰ)求证:AB⊥CD;
(Ⅱ)已知A1D=10,A1A2=8,求二面角A-BC-D的余弦值。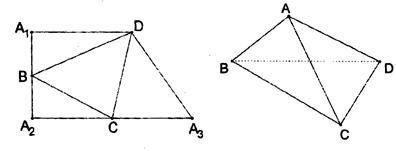
(I)由题意 ,故
,故 平面
平面 ,所以
,所以 …5分
…5分
(II)由条件,如图建立坐标系,平面 的法向量为
的法向量为 ,
,
设平面 的法向量为
的法向量为 ,又
,又 ,
,
故有 ,
,
设二面角 的大小为
的大小为 ,则
,则 …………15分
…………15分
解析

练习册系列答案
相关题目
如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成二面角的余弦值为( )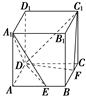
A.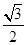 | B.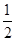 | C.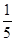 | D.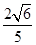 |
若两点的坐标是A(3cosα,3sinα,1),B(2cosβ,2sinβ,1),则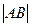 的取值范围是( )
的取值范围是( )
| A.[0,5] |
| B.[1,25] |
| C.(0,5) |
| D.[1,5] |
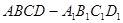 中,
中,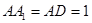 ,
,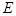 为
为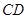 中点.
中点.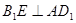 ;
;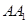 上是否存在一点
上是否存在一点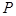 ,使得
,使得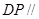 平面
平面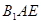 ?若存在,求
?若存在,求 的长;若不存在,说明理由.
的长;若不存在,说明理由.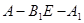 的大小为
的大小为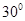 ,求
,求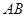 的长.
的长.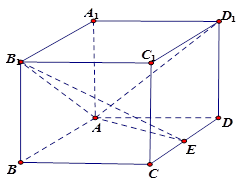
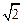 .M为线段PC的中点.
.M为线段PC的中点.
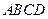 中,
中,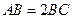 ,
,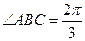 ,
,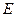 为线段
为线段 的中线,将△
的中线,将△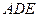 沿
沿 直线
直线 翻折成△
翻折成△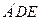 ,使平面
,使平面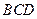 ,
,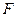 为线
为线 段
段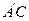 的中点.
的中点. ∥平面
∥平面 为线段
为线段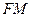 与平面
与平面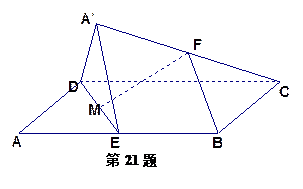

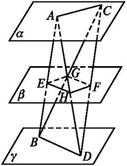
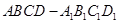 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点