题目内容
已知动直线l的倾斜角为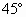 ,若l与抛物线
,若l与抛物线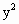 =2px(p>0)交于A、B两点,且A、B两点的纵坐标之和为2.
=2px(p>0)交于A、B两点,且A、B两点的纵坐标之和为2.
(Ⅰ)求抛物线的方程;
(Ⅱ)若直线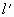 与l平行,且
与l平行,且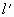 过抛物线的准线与x轴的交点,M为抛物线上一动点,求M点到直线
过抛物线的准线与x轴的交点,M为抛物线上一动点,求M点到直线 的最小距离;
的最小距离;
(Ⅲ)线段AB的中垂线交x轴于P点,当点P关于直线l的对称点落在抛物线上时,求直线l的方程.
(Ⅳ)若直线l过抛物线的焦点,求△OAB的面积(O为坐标原点).
答案:
解析:
解析:
|
(1)设直线l的方程为y=x+b ∴抛物线的方程是: (2)抛物线 ∵ 设M的坐标为( ∴当y=1时, (3)抛物线 ∴直线l的方程为y=x- (4) ∴ ∴|AB|= 点(0,0)到l的距离d ∴
|

练习册系列答案
相关题目
 =2p(y-b)
=2p(y-b) -2py+2pb=0,此方程两实根y1、y2满足
-2py+2pb=0,此方程两实根y1、y2满足 =2p,由已知得2p=2
=2p,由已知得2p=2 =1
=1 =2x
=2x
 ∥l,∴
∥l,∴ 的方程为y=x+
的方程为y=x+ 2x-2y+1=0
2x-2y+1=0 ,y),则M到
,y),则M到 的距离为:
的距离为:
 =0
=0 =2x的焦点坐标为F(
=2x的焦点坐标为F( ,0)
,0)
 =3
=3 +p=3+1=4
+p=3+1=4
 ·d·|AB|=
·d·|AB|=
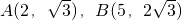 ,直线l的倾斜角是直线AB倾斜角的两倍,则直线l的斜率为________.
,直线l的倾斜角是直线AB倾斜角的两倍,则直线l的斜率为________. ,直线l的倾斜角是直线AB倾斜角的两倍,则直线l的斜率为 .
,直线l的倾斜角是直线AB倾斜角的两倍,则直线l的斜率为 .