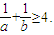题目内容
(1)已知a>0,b>0,求证:
≥
;
(2)已知a>1,b>1,且a>b,试比较a+
与b+
的大小.
|
| a+b |
| 2 |
(2)已知a>1,b>1,且a>b,试比较a+
| 1 |
| a |
| 1 |
| b |
分析:(1)由基本不等式得到2(a2+b2)≥a2+2ab+b2进一步有:
≥
;
(2)由于a+
-(b+
)=(a-b)+(
-
)=(a-b)+
=(a-b)(1-
)=(a-b)•
,下面利用条件证明(a-b)•
>0即可.
|
| a+b |
| 2 |
(2)由于a+
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| b-a |
| ab |
| 1 |
| ab |
| ab-1 |
| ab |
| ab-1 |
| ab |
解答:解:(1)a2+b2≥2ab⇒2(a2+b2)≥a2+2ab+b2
⇒2(a2+b2)≥(a+b)2⇒
≥(
)2…(3分)
由于a>0,b>0⇒a+b>0,故
≥
…(4分)
(2)解:由于a+
-(b+
)=(a-b)+(
-
)
=(a-b)+
=(a-b)(1-
)=(a-b)•
,…(8分)
因为a>1,b>1⇒ab>1⇒ab-1>0且ab>0,又a>b⇒a-b>0,
所以(a-b)•
>0.
故a+
>b+
…(10分)
⇒2(a2+b2)≥(a+b)2⇒
| a2+b2 |
| 2 |
| a+b |
| 2 |
由于a>0,b>0⇒a+b>0,故
|
| a+b |
| 2 |
(2)解:由于a+
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
=(a-b)+
| b-a |
| ab |
| 1 |
| ab |
| ab-1 |
| ab |
因为a>1,b>1⇒ab>1⇒ab-1>0且ab>0,又a>b⇒a-b>0,
所以(a-b)•
| ab-1 |
| ab |
故a+
| 1 |
| a |
| 1 |
| b |
点评:本题主要考查了基本不等式、不等式比较大小,属于基础题,解答的关键是需要同学们对不等式的证明方法非常熟练.

练习册系列答案
相关题目