题目内容
(1)已知a>0,b>0,a+b=1,求证: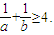
(2)证明:a4+b4+c4+d4≥4abcd.
【答案】分析:(1)利用a+b=1将要证不等式中的1代换,即可得证.
(2)利用a2+b2≥2ab两两结合即可求证,但需两次利用不等式,注意等号成立的条件.
解答:解:(1)方法一:∵a>0,b>0,a+b=1
∴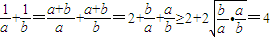
(当且仅当a=b= 时等号成立).∴
时等号成立).∴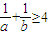 .∴原不等式成立.
.∴原不等式成立.
方法二:∵a>0,b>0,a+b=1,
∴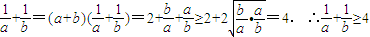
(当且仅当a=b= 时等号成立).∴原不等式成立.
时等号成立).∴原不等式成立.
(2)a4+b4+c4+d4≥2a2b2+2c2d2=2(a2b2+c2d2)≥2•2abcd=4abcd.
故原不等式得证,等号成立的条件是a2=b2且c2=d2且a2b2=c2d2.
点评:本题考查了利用均值不等式证明不等式,灵活运用了“1”的代换,同时要注意等号成立的条件.
(2)利用a2+b2≥2ab两两结合即可求证,但需两次利用不等式,注意等号成立的条件.
解答:解:(1)方法一:∵a>0,b>0,a+b=1
∴
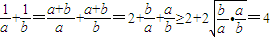
(当且仅当a=b=
 时等号成立).∴
时等号成立).∴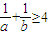 .∴原不等式成立.
.∴原不等式成立.方法二:∵a>0,b>0,a+b=1,
∴
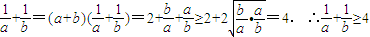
(当且仅当a=b=
 时等号成立).∴原不等式成立.
时等号成立).∴原不等式成立.(2)a4+b4+c4+d4≥2a2b2+2c2d2=2(a2b2+c2d2)≥2•2abcd=4abcd.
故原不等式得证,等号成立的条件是a2=b2且c2=d2且a2b2=c2d2.
点评:本题考查了利用均值不等式证明不等式,灵活运用了“1”的代换,同时要注意等号成立的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目