题目内容
已知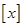 表示不超过实数
表示不超过实数 的最大整数
的最大整数 ,如:
,如: .定义
.定义 ,给出如下命题:
,给出如下命题:
① 使 成立的
成立的 的取值范围是
的取值范围是 ;
;
② 函数 的定义域为
的定义域为 ,值域为
,值域为 ;
;
③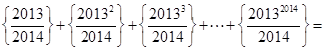 1007;
1007;
④ 设函数 ,则函数
,则函数 的不同零点有3个.其中正确的命题有
的不同零点有3个.其中正确的命题有
| A.1个 | B.2个 | C.3个 | D.4个 |
C
解析试题分析:①由题意知[x+1]=3时,有x+1≥3 X+1<4,解得即可;
②由题意[x]≤x<[x]+1,得x-[x]的取值范围,即{x}的值域;
③观察
④由题意0≤f(x)<1,讨论0≤x<1,x≥1和x<0时, 的零点情况.
的零点情况.
考点:(1)命题的真假判断与应用;(2)根的存在性及根的个数判断.

练习册系列答案
相关题目
已知集合 ,
, ,若“
,若“ ”是“
”是“ ”的充分非必要条件,则
”的充分非必要条件,则 的取值范围是( ).
的取值范围是( ).
A. | B. | C. | D. |
已知命题P:存在 ;命题q:任意
;命题q:任意 ,则下列命题为真命题的是( )
,则下列命题为真命题的是( )
A. | B. | C. | D. |
设 为非零实数,则p:
为非零实数,则p: 是q:
是q: 成立的 ( )
成立的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
设 ,则
,则 是
是 的( ).
的( ).
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题正确的是
A.“ ”是“ ”是“ ”的必要不充分条件 ”的必要不充分条件 |
B.对于命题p: ,使得 ,使得 ,则 ,则 : : 均有 均有 |
C.若 为假命题,则 为假命题,则 均为假命题 均为假命题 |
D.命题“若 ,则 ,则 ”的否命题为“若 ”的否命题为“若 则 则 |
设函数 及其导函数
及其导函数 都是定义在R上的函数,则“
都是定义在R上的函数,则“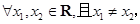
 ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
己知命题 “ ”是假命题,则实数
”是假命题,则实数 的取值范围是( )
的取值范围是( )
A. | B.(?1,3) | C. | D.(?3,1) |
已知命题 ,那么
,那么 是
是
A. | B. | C. | D. |