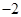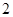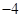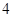题目内容

已知F1，F2分别是椭圆的左，右焦点，现以F2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M，N，若过F1的直线MF1是圆F2的切线，则椭圆的离心率为（　　）
A．
3
-1		B．2-
3
C．
2
2
D．
3
2
∵F1，F2分别是椭圆的左，右焦点，
现以F2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M，N，
过F1的直线MF1是圆F2的切线，
∴|MF2|=c，|F1F2|=2c，∠F1MF2=90°，
∴|MF1|=
4c2-c2
=
3
c，
∴2a=
3
c+c=(
3
+1)c，
∴椭圆的离心率e=
c
a
=
2
3
+1
=
3
-1．
故选：A．
练习册系列答案
相关题目
设椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)恒过定点A（1，2），则椭圆的中心到准线的距离的最小值______．
设椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的两焦点为F1、F2，若椭圆上存在一点Q，使∠F1QF2=120°，椭圆离心率e的取值范围为（　　）
A．
3
2
≤e＜1		B．
6
3
＜e＜1		C．0＜e≤
6
3
D．
1
2
＜e＜1
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0），A为左顶点，B为短轴一顶点，F为右焦点且AB⊥BF，则这个椭圆的离心率等于______．
若P为椭圆
x2
9
+
y2
6
=1上一点，F1和F2为椭圆的两个焦点，∠F1PF2=60°，则|PF1|•|PF2|的值为______．
已知椭圆的中心在原点，其中一个焦点为F1（
3
，0），且该焦点于长轴上较近的端点距离为2-
3
．
（1）示此椭圆的标准方程及离心率；
（2）设F2是椭圆另一个焦点，若P是该椭圆上一个动点，求
PF1
•
PF2
的取值范围．
椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的一个焦点为F1，若椭圆上存在一个点P，满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点，则椭圆的离心率为______．
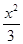已知双曲线－y2＝1的左，右焦点分别为F1，F2，点P在双曲线上，且满足|PF1|＋|PF2|＝2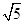，则△PF1F2的面积为(　　)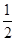
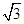
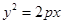A．B．1C．D．
若抛物线的焦点与双曲线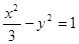的右焦点重合，则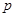的值为（    ）．
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网