题目内容
1)设函数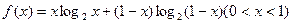 ,求
,求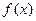 的最小值;
的最小值;
(2)设正数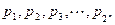 满足
满足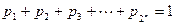 ,
,
求证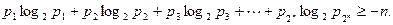
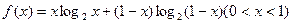 ,求
,求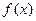 的最小值;
的最小值;(2)设正数
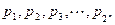 满足
满足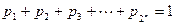 ,
,求证
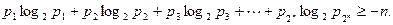
(1) 时取得最小值,
时取得最小值, ;(2)同解析;
;(2)同解析;
 时取得最小值,
时取得最小值, ;(2)同解析;
;(2)同解析;(1)对函数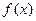 求导数:
求导数:



于是
当 在区间
在区间 是减函数,
是减函数,
当 在区间
在区间 是增函数.
是增函数.
所以 时取得最小值,
时取得最小值, ,
,
(Ⅱ)(i)当n=1时,由(Ⅰ)知命题成立.
(ii)假定当 时命题成立,即若正数
时命题成立,即若正数 ,
,
则
当 时,若正数
时,若正数
令
则 为正数,且
为正数,且
由归纳假定知

 ①
①
同理,由 可得
可得
 ②
②
综合①、②两式

即当 时命题也成立.
时命题也成立.
根据(i)、(ii)可知对一切正整数n命题成立.
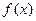 求导数:
求导数:


于是

当
 在区间
在区间 是减函数,
是减函数,当
 在区间
在区间 是增函数.
是增函数.所以
 时取得最小值,
时取得最小值, ,
,(Ⅱ)(i)当n=1时,由(Ⅰ)知命题成立.
(ii)假定当
 时命题成立,即若正数
时命题成立,即若正数 ,
,则

当
 时,若正数
时,若正数
令

则
 为正数,且
为正数,且
由归纳假定知


 ①
①同理,由
 可得
可得
 ②
②综合①、②两式


即当
 时命题也成立.
时命题也成立.根据(i)、(ii)可知对一切正整数n命题成立.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
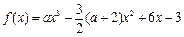 .
.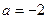 时,求函数
时,求函数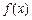 的单调区间和极值;
的单调区间和极值; 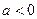 时,试求方程
时,试求方程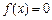 根的个数.
根的个数.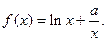
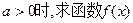 的单调区间;
的单调区间;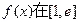 上的最小值为1,求实数a的取值范围;(其中e为自然对数的底数)
上的最小值为1,求实数a的取值范围;(其中e为自然对数的底数)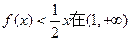 上恒成立,求实数a的取值范围。
上恒成立,求实数a的取值范围。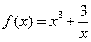 ,求函数f(x)的单调区间及其极值.
,求函数f(x)的单调区间及其极值.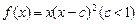 在区间
在区间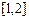 上的最小值为4,求
上的最小值为4,求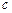 的值.
的值.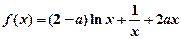 (a∈R).
(a∈R).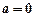 时,求
时,求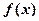 的极值;
的极值;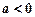 时,求
时,求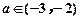 及
及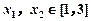 ,恒有
,恒有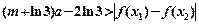
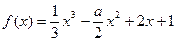 且
且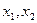 是
是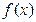 的两个极值点,
的两个极值点,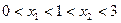 ,
,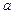 的取值范围;
的取值范围;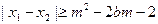 ,对
,对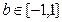 恒成立。求实数
恒成立。求实数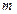 的取值范围;
的取值范围;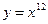 ;(2)
;(2)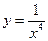 ;(3)
;(3)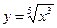 .
.