题目内容
18.已知函数f(x)=2log22x-4λlog2x-1在x∈[1,2]上的最小值是-$\frac{3}{2}$,则实数λ的值为( )| A. | λ=-1 | B. | λ=$\frac{1}{2}$ | C. | λ=$\frac{5}{8}$ | D. | λ=$\frac{7}{16}$ |
分析 可设t=log2x(0≤t≤1),即有g(t)=2t2-4λt-1在[0,1]上的最小值是-$\frac{3}{2}$,求出对称轴,讨论对称轴和区间[0,1]的关系,运用单调性可得最小值,解方程可得所求值.
解答 解:可设t=log2x(0≤t≤1),
即有g(t)=2t2-4λt-1在[0,1]上的最小值是-$\frac{3}{2}$,
对称轴为t=λ,
①当λ≤0时,[0,1]为增区间,即有g(0)为最小值,且为-1,不成立;
②当λ≥1时,[0,1]为减区间,即有g(1)为最小值,
且为1-4λ=-$\frac{3}{2}$,解得λ=$\frac{5}{8}$,不成立;
③当0<λ<1时,[0,λ)为减区间,(λ,1)为增区间,
即有g(λ)取得最小值,且为2λ2-4λ2-1=-$\frac{3}{2}$,解得λ=$\frac{1}{2}$(负的舍去).
综上可得,$λ=\frac{1}{2}$.
故选B.
点评 本题考查可化为二次函数的最值的求法,注意运用换元法和对数函数的单调性,讨论二次函数的对称轴和区间的关系,考查运算能力,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
9.函数f(x)=loga(ax-2)在[1,3]上单调递增,则a的取值范围是( )
| A. | (1,+∞) | B. | (0,2) | C. | (0,$\frac{2}{3}$) | D. | (2,+∞) |
13.集合A={x|y=log2(x+1)},B={-1,0,1},则A∩B等于( )
| A. | {0,1} | B. | {-1,0,1} | C. | {0} | D. | {1} |
3.已知等比数列{an},{bn}的公比分别为q1,q2,则q1=q2是{an+bn}为等比数列的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
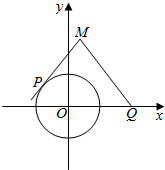 已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1.动点M到圆的切线长等于|MQ|的2倍.
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1.动点M到圆的切线长等于|MQ|的2倍.