题目内容
3.设P为△ABC所在平面上一点,且满足$3\overrightarrow{PA}+4\overrightarrow{PC}=m\overrightarrow{AB}$(m>0).若△ABP的面积为8,则△ABC的面积为14.分析 由题意可得$\frac{3}{7}$$\overrightarrow{PA}$+$\frac{4}{7}$$\overrightarrow{PC}$=$\frac{m}{7}$$\overrightarrow{AB}$,即有D在线段AC上,C到直线AB的距离等于P到直线AB的距离的$\frac{7}{4}$倍,故S△ABC=$\frac{7}{4}$S△ABP,结合已知中△ABP的面积为8,即可得到答案.
解答 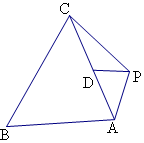 解:由3$\overrightarrow{PA}$+4$\overrightarrow{PC}$=m$\overrightarrow{AB}$,
解:由3$\overrightarrow{PA}$+4$\overrightarrow{PC}$=m$\overrightarrow{AB}$,
可得$\frac{3}{7}$$\overrightarrow{PA}$+$\frac{4}{7}$$\overrightarrow{PC}$=$\frac{m}{7}$$\overrightarrow{AB}$,
可设$\overrightarrow{PD}$=$\frac{3}{7}$$\overrightarrow{PA}$+$\frac{4}{7}$$\overrightarrow{PC}$,
则D,A,C共线,且D在线段AC上,
可得$\overrightarrow{PD}$=$\frac{m}{7}$$\overrightarrow{AB}$,
即有D分AC的比为4:3,
即有C到直线AB的距离等于P到直线AB的距离的$\frac{7}{4}$倍,
故S△ABC=$\frac{7}{4}$S△ABP=$\frac{7}{4}$×8=14.
故答案为:14.
点评 本题考查向量共线定理的运用,以及三点共线的坐标表示,考查三角形的面积的求法,注意运用比例法,考查运算能力,属于中档题.

练习册系列答案
相关题目
13.已知tanα=-$\frac{3}{4}$,且α∈(0,π),则cosα=( )
| A. | $\frac{4}{5}$ | B. | $\frac{1}{2}$ | C. | -$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
12. 如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC、MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC、MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
 如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC、MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC、MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{11}$ | D. | $\frac{4}{13}$ |
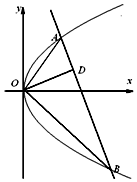 如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).
如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).