题目内容
2.正三棱台上、下底面边长分别是a和2a,棱台的高为$\frac{\sqrt{33}}{6}$a,则正三棱台的侧面积为$\frac{9}{2}$a2.分析 作出三棱台的直观图,还原成三棱锥,利用图中的相似及直角三角形关系求出棱台的侧棱,再求出侧面梯形的高即可算出答案.
解答 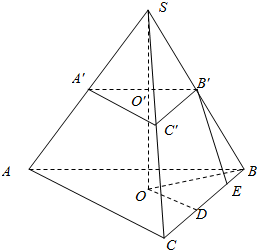 解:作出三棱台的直观图,还原成三棱锥如图:
解:作出三棱台的直观图,还原成三棱锥如图:
取BC中点D,连接OD,OB,则BD=$\frac{1}{2}BC$=a,∠ODB=90°,∠OBD=30°.
∴OB=2OD
∵OD2+BD2=OB2
∴OB=$\frac{2\sqrt{3}a}{3}$
∵$\frac{SO'}{SO}$=$\frac{SB′}{SB}$=$\frac{B'C'}{BC}$=$\frac{a}{2a}$=$\frac{1}{2}$
∴SO=2SO'=$\frac{\sqrt{33}a}{3}$,
∴SB=$\sqrt{S{O}^{2}+O{B}^{2}}$=$\sqrt{5}a$,
∴B'B=$\frac{\sqrt{5}a}{2}$.
过B'作B'E⊥BC于E,
则BE=$\frac{1}{2}$(BC-B'C')=$\frac{1}{2}a$.
∴B'E=$\sqrt{B'{B}^{2}-B{E}^{2}}$=a.
即棱台侧面梯形的高为a.
∴S侧面积=$\frac{1}{2}$(a+2a)•a•3=$\frac{9{a}^{2}}{2}$.
故答案为$\frac{9{a}^{2}}{2}$.
点评 本题考查了棱台的结构特征,面积计算,属于基础题.

练习册系列答案
相关题目
11.设函数f(x)=$\sqrt{3}$asinωxcosωx+acos2ωx-$\frac{1}{2}$(ω>0,a>0)的最大值为1,且其图象相邻两条对称轴的距离为$\frac{π}{2}$,若将函数f(x)的图象向右平移$\frac{π}{12}$个单位,所得图象对应函数为g(x),则( )
| A. | f(x)的图象关于直线x=$\frac{π}{3}$对称,g(x)图象关于原点对称 | |
| B. | f(x)的图象关于点($\frac{π}{4}$,0)对称,g(x)图象关于直线x=$\frac{π}{4}$对称 | |
| C. | f(x)的图象关于直线x=$\frac{π}{6}$对称,g(x)图象关于原点对称 | |
| D. | f(x)的图象关于点($\frac{5π}{12}$,0)对称,g(x)图象关于直线x=$\frac{π}{6}$对称 |
12.已知0<a<b<1,e是自然对数的底数,则正确的是( )
| A. | ${(\frac{1}{e})^a}<{(\frac{1}{e})^b}$ | B. | 3b<3a | C. | (lga)2<(lgb)2 | D. | loga3>logb3 |