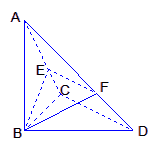
题目内容
已知![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 分别是
分别是![]() 上的动点,且
上的动点,且![]() :
:
(1)求证:不论![]() 为何值,总有平面
为何值,总有平面![]() 平面
平面![]() ;
;
(2)当![]() 为何值时,平面
为何值时,平面![]() 平面
平面![]() ?
?
(1)同解析,(2)![]() 时,平面
时,平面![]() 平面
平面![]() .
.
解析:
(1)∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 且
且![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() ,
,
∴不论![]() 为何值,恒有
为何值,恒有![]() ,
,
∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴不论![]() 为何值恒有平面
为何值恒有平面![]() ⊥平面
⊥平面![]() .
.
(2)由(1)知,![]() ,又平面
,又平面![]() ⊥平面
⊥平面![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]()
∴![]() 由
由![]() ,得
,得![]()
![]() ,
,
故当![]() 时,平面
时,平面![]() 平面
平面![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断:
如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断: 已知
已知