题目内容
已知a>0,函数y=f(x)=x3-ax在[1,+∞)上是一个单调函数.
(1)试问函数y=f(x)在a>0的条件下,在[1,+∞)上能否是单调递减函数?请说明理由;
(2)若f(x)在区间[1,+∞)上是单调递增函数,试求出实数a的取值范围;
(3)设x0≥1,f(x0)≥11且f[f(x0)]=x0,求证:f(x0)=x0.
答案:
解析:
解析:
|
(1)若 (2)若 若 若 故只有 证法二:设 ∵ |

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目

 设0<
设0< <
< ,记曲线y=
,记曲线y= 在点
在点 处的切线为L,
处的切线为L, ,证明:①
,证明:①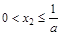 ; ②若
; ②若 ,则
,则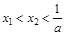 。
。