题目内容
在△ABC中,sinA>sinB是A>B的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
C.
解析试题分析:在△ABC中,由正弦定理得 ,若A>B,即a>b,则sinA>sinB;若sinA>sinB,则a>b,即A>B,所以sinA>sinB是A>B的充要条件.
,若A>B,即a>b,则sinA>sinB;若sinA>sinB,则a>b,即A>B,所以sinA>sinB是A>B的充要条件.
考点:充要条件及正弦定理.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
设 且
且 ,则“函数
,则“函数 ”在R上是增函数”是“函数
”在R上是增函数”是“函数 ”“在
”“在 上是增函数”的( )
上是增函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列说法正确的是( )
A.命题“  , , ”的否定是“ ”的否定是“  , , ” ” |
B.命题“已知  ,若 ,若 ,则 ,则 或 或 ”是真命题 ”是真命题 |
C.“ 在 在 上恒成立” 上恒成立” “ “ 在 在 上恒成立” 上恒成立” |
D.命题“若 ,则函数 ,则函数 只有一个零点”的逆命题为真命题 只有一个零点”的逆命题为真命题 |
p:|x|>2是q:x<﹣2的( )条件
| A.充分必要 | B.充分不必要 |
| C.必要不充分 | D.既不充分也不必要 |
已知直线 与
与 ,给出命题P:
,给出命题P: 的充要条件是
的充要条件是
 ;命题q:
;命题q: 的充要条件是
的充要条件是 .对以上两个命题,下列结论中正确的是:( )
.对以上两个命题,下列结论中正确的是:( )
| A.命题“p且q"为真 | B.命题“p或q”为假 |
C.命题“p或 q"为假 q"为假 | D.命题“p且 q"为真 q"为真 |
已知命题 ,其中正确的是 ( )
,其中正确的是 ( )
A. | B. |
C. | D. |
设 ,则
,则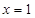 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若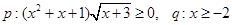 ,则p是q的 ( )
,则p是q的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
 “
“ ,使得
,使得 ”,则
”,则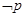 是假命题.
是假命题. ,则
,则 ,
, 互为相反数”的逆命题为假命题.
互为相反数”的逆命题为假命题. ”,则
”,则 ”.
”.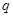 ”的逆否命题是“若
”的逆否命题是“若 ,则
,则 ”.
”.