题目内容
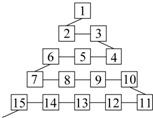
 如图是从事网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推.若2013是第m行从左至右算的第n个数字,则(m,n)为( )
如图是从事网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推.若2013是第m行从左至右算的第n个数字,则(m,n)为( )分析:每行的行号数和这一行的数字的个数相同,奇数行的数字从左向右依次减小,偶数行的数字从左向右依次增大,每行中相邻的数字为连续正整数,由此结合等差数列的求和公式可得第63行最左边的一个数,进而可得答案.
解答:解:由每行的行号数和这一行的数字的个数相同,奇数行的数字从左向右依次减小,
偶数行的数字从左向右依次增大,可得第63行的数字从左向右依次减小,
可求出第63行最左边的一个数是
=2016,
从左至右的第4个数应是2016-3=2013.
故2013在第63行,第4列,
故选B.
偶数行的数字从左向右依次增大,可得第63行的数字从左向右依次减小,
可求出第63行最左边的一个数是
| 63×(63+1) |
| 2 |
从左至右的第4个数应是2016-3=2013.
故2013在第63行,第4列,
故选B.
点评:本题考查合情推理,涉及等差数列,确定第63行最左边的一个数是关键,属基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 如图是从事网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推.则第99行从左至右算第3个数字是
如图是从事网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推.则第99行从左至右算第3个数字是 如图是从事网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推.则第27行从左至右算第8个数字是
如图是从事网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推.则第27行从左至右算第8个数字是 (2008•宝坻区一模)如图是从事网络工作者经常用来解释网络运作的蛇形模型,数字1出现在第1行;数字2、3出现在第2行;数字6、5、4(从左至右)出现在第3行;数字7、8、9、10出在第4行;依此类推.试问第50行,从左至右算,第7个数字为
(2008•宝坻区一模)如图是从事网络工作者经常用来解释网络运作的蛇形模型,数字1出现在第1行;数字2、3出现在第2行;数字6、5、4(从左至右)出现在第3行;数字7、8、9、10出在第4行;依此类推.试问第50行,从左至右算,第7个数字为