题目内容
17.设数列{an}的前n项的和为Sn,且$\left\{{\frac{S_n}{n}}\right\}$是等差数列,已知a1=1,$\frac{S_2}{2}+\frac{S_3}{3}+\frac{S_4}{4}$=12.(Ⅰ)求$\left\{{\frac{S_n}{n}}\right\}$的通项公式;
(Ⅱ)求{an}的通项公式an;
(Ⅲ)当n≥2时,an+1+$\frac{λ}{a_n}$≥λ恒成立,求λ的取值范围.
分析 (Ⅰ)利用等差中项可知3•$\frac{{S}_{3}}{3}$=12即$\frac{{S}_{3}}{3}$=4,进而计算可得结论;
(Ⅱ)通过$\frac{{S}_{n}}{n}$=$\frac{3}{2}$n-$\frac{1}{2}$可知Sn=$\frac{3}{2}$n2-$\frac{1}{2}$n,利用an=Sn-Sn-1计算即得结论;
(Ⅲ)通过an=3n-2,问题转化为求bn=$\frac{(3n+1)(3n-2)}{3(n-1)}$的最小值,利用作差法可知bn+1>bn,进而计算可得结论.
解答 解:(Ⅰ)∵a1=1,∴$\frac{{S}_{1}}{1}$=1,
又∵$\frac{S_2}{2}+\frac{S_3}{3}+\frac{S_4}{4}$=12,
∴3•$\frac{{S}_{3}}{3}$=12,即$\frac{{S}_{3}}{3}$=4,
∴公差d=$\frac{1}{2}$($\frac{{S}_{3}}{3}$-$\frac{{S}_{1}}{1}$)=$\frac{3}{2}$,
∴$\frac{{S}_{n}}{n}$=1+$\frac{3}{2}$(n-1)=$\frac{3}{2}$n-$\frac{1}{2}$;
(Ⅱ)∵$\frac{{S}_{n}}{n}$=$\frac{3}{2}$n-$\frac{1}{2}$,
∴Sn=$\frac{3}{2}$n2-$\frac{1}{2}$n,
∴an=Sn-Sn-1
=($\frac{3}{2}$n2-$\frac{1}{2}$n)-[$\frac{3}{2}$(n-1)2-$\frac{1}{2}$(n-1)]
=3n-2(n≥2),
又∵a1=1满足上式,
∴an=3n-2;
(Ⅲ)∵an=3n-2,
∴an+1+$\frac{λ}{a_n}$≥λ恒成立等价于3n+1+$\frac{λ}{3n-2}$≥λ,
即λ≤$\frac{(3n+1)(3n-2)}{3(n-1)}$,
记bn=$\frac{(3n+1)(3n-2)}{3(n-1)}$,
∵bn+1-bn=$\frac{(3n+1)(3n+4)}{3n}$-$\frac{(3n+1)(3n-2)}{3(n-1)}$=$\frac{(3n+1)(3n-2)}{3n(n-1)}$>0,
∴数列{bn}的最小值为b2=$\frac{28}{3}$,
∴$λ≤\frac{28}{3}$.
点评 本题考查数列的通项,考查运算求解能力,注意解题方法的积累,属于中档题.

 的单调递增区间是( )
的单调递增区间是( ) B.
B. C.
C.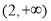 D.
D.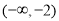
 .
.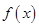 最小正周期;
最小正周期;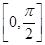 上的最大值和最小值.
上的最大值和最小值.