题目内容

关于实数x的不等式|x-|≤与x2-3(a+1)x+2(3a+1)≤0(其中a∈R)的解集依次记为A与B.求使AB的a的取值范围.

解：由|x-|≤得-≤x-≤，

∴2a≤x≤a2+1,即A＝｛x|2a≤x≤a2+1｝.

又不等式x2-3(a+1)x+2(3a+1)≤0,可化为（x-2）［x-(3a+1)］≤0.

(1)当3a+1＜2,即a＜时，3a+1≤x≤2,即B={x|3a+1≤x≤2}.

∴AB,即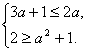

∴a=-1.

(2)当3a+1=2, 即a=时，x=2,B={2},此时AB不成立.

(3)当3a+1＞2,即a＞时，2≤x≤3a+1,B={x|2≤x≤3a+1}.

∵AB,即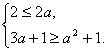

∴1≤a≤3.

综上所述，a的取值范围是{a|1≤a≤3或a=-1}.


练习册系列答案
相关题目
关于实数x的不等式|x-
1
2
(a+1)2|≤
1
2
(a-1)2与x2-3(a+1)x+2(3a+1)≤0的解集依次为A与B，求使A⊆B的a的取值范围．
解关于实数x的不等式
axx-1
＜1，a∈R．
已知函数f（x）的定义域为（-2，2），其导函数f′（x）=x2+2cosx且f（0）=0，则关于实数x的不等式f（x-2）+f（x2-2x）＞0的解集为（　　）
已知函数f（x）（x∈R）的最小正周期为2，且对任意实数x，f（2-x）=f（2+x），且[a，b]（a＜b）是f（x）的一个单调区间．
（1）求证：b-a≤1；
（2）已知区间[0，1]为f（x）的一个单调区间，且对任意x＜0，都有f（2x）＞f（2），解关于实数x的不等式f（-10.5）＞f（x2+6x）．
（2009•天门模拟）关于实数x的不等式|1-
1
x
|＞1的解集是
（-∞，0）∪（0，
1
2
）
（-∞，0）∪（0，
1
2
）
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网