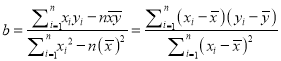题目内容
【题目】定义：在数列
中，若
为常数）则称为“等方差数列”，下列是对“等方差数列”的有关判断（ ）
①若是“等方差数列”，在数列
是等差数列；
②
是“等方差数列”；
③若是“等方差数列”，则数列
为常）也是“等方差数列”；
④若既是“等方差数列”又是等差数列，则该数列是常数数列.
其中正确命题的个数为( )
A. 
B. 
C. 
D. 
【答案】B
【解析】①：可以举反例。如an=0时数列
不存在，所以①错误；
②：对数列{(2)n}有
不是常数，所以②错误
③：对数列{akn}有
，
而k，p均为常数，所以数列{akn}也是“等方差数列”，所以③正确；
④：设数列{an}首项a1，公差为d则有a2=a1+d，a3=a1+2d，所以有(a1+d)2a21=p，且(a1+2d)2(a1+d)2=p，所以得d2+2a1d=p，3d2+2a1d=p，两式相减得d=0，所以此数列为常数数列，所以④正确。
本题选择B选项.
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
