题目内容
6.已知实数a>0,函数$f(x)=\left\{\begin{array}{l}{e^{x-1}}+a,x<0\\{e^{x-}}+\frac{a}{2}{x^2}-(a+1)x+a,x≥0\end{array}\right.$,其中e是自然对数的底数,若函数y=f(x)与y=f[f(x)]有相同的值域,则实数a的取值范围是( )| A. | (0,2] | B. | [1,2] | C. | (0,1] | D. | [1,e] |
分析 利用导数结合图象求出函数f(x)的值域,再由函数y=f(x)与y=f[f(x)]有相同的值域可得$\frac{a}{2}≤1$,从而求得a的取值范围.
解答 解:当x<0时,f(x)在(-∞,0)上单调递增,且x→-∞时,f(x)→a;
当x≥0时,f′(x)=ex-1+ax-a-1,
∴f′(x)是增函数,且f′(1)=0,
∴当0<x<1时,f′(x)<0,当x>1时,f′(x)>0,
∴f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
又f(1)=$\frac{a}{2}$,当x→+∞时,f(x)→+∞,
作出f(x)的大致函数图象如图所示: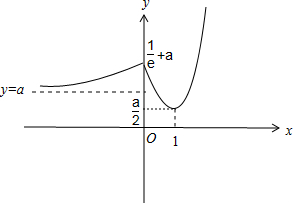
由图象可知f(x)≥$\frac{a}{2}$,即函数y=f(x)的值域为[$\frac{a}{2}$,+∞).
∵y=f[f(x)]的值域也是[$\frac{a}{2}$,+∞).
∴$\frac{a}{2}≤1$,得a≤2.
∴实数a的取值范围是(0,2].
故选:A.
点评 本题考查了函数零点与函数图象的关系,函数单调性的判断与极值计算,体现了数形结合的解题思想方法,属于中档题.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
3.已知全集为R,集合M={-1,0,1,5},N={x|x2-x-2<0},则M∩N=( )
| A. | {0,1,5} | B. | {-1,0,1} | C. | {0,1} | D. | {-1,1} |
14.已知a=3${\;}^{\frac{4}{3}}$,b=($\frac{1}{2}$)${\;}^{\frac{2}{3}}$,c=log2$\frac{1}{3}$,那么( )
| A. | b<a<c | B. | a<b<c | C. | c<b<a | D. | c<a<b |
1.设等差数列{an}满足$\frac{si{n}^{2}{a}_{2}-co{s}^{2}{a}_{2}+co{s}^{2}{a}_{2}co{s}^{2}{a}_{7}-si{n}^{2}{a}_{2}si{n}^{2}{a}_{7}}{sin({a}_{1}+{a}_{8})}$=1,公差d∈(-1,0),若当且仅当n=11时,数列{an}的前n项和Sn取得最大值,则首项a1的取值范围是( )
| A. | ($\frac{9π}{10}$,π) | B. | [π,$\frac{11π}{10}$] | C. | [$\frac{9π}{10}$,π] | D. | (π,$\frac{11π}{10}$) |
15.函数y=log2(x+1)的定义域是( )
| A. | (0,+∞) | B. | (-1,+∞) | C. | (1,+∞) | D. | [-1,+∞) |
13.已知集合 A={x∈R|(x-1)(x-3)≤0},B={-1,1,2,3},则A∩B等( )
| A. | {1,2} | B. | {2,3} | C. | {1,2,3} | D. | {-1,1,2,3} |