题目内容
14.设命题p:关于x的函数y=(a-1)x为增函数;命题q:不等式-x2+2x-2≤a对一切实数均成立.(1)若命题q为真命题,求实数a的取值范围;
(2)命题“p或q”为真命题,且“p且q”为假命题,求实数a的取值范围.
分析 (1)根据二次函数的性质求出a的范围即可;(2)根据命题p、q一真一假,得到关于a的不等式组,解出即可.
解答 解:(1)当命题q为真命时,∴-1≤a
∴实数a的取值范围是[-1,+∞);…(4分)
(2)由命题“p或q”为真,且“p且q”为假,得命题p、q一真一假
①当p真q假时,则$\left\{\begin{array}{l}a>1\\ a<-1\end{array}\right.$,无解;…(7分)
②当p假q真时,则$\left\{\begin{array}{l}a≤1\\ a≥-1\end{array}\right.$,得-1≤a≤1,
∴实数a的取值范围是[-1,1].…(10分)
点评 本题考查了复合命题的判断,考查函数的单调性以及二次函数的性质,是一道基础题.

练习册系列答案
相关题目
5.执行如图的框图,第3次和最后一次输出的A的值是( )
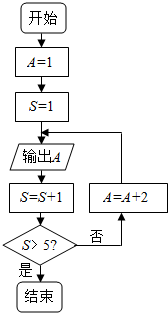

| A. | 7,9 | B. | 5,11 | C. | 7,11 | D. | 5,9 |
2.若定义在R上的函数f(x)满足f(0)=-1,g(x)=f(x)-kx,h(x)=f(x)-x,且函数g(x)与函数h(x)在R上均单调递增,当k>l时,则下列结论中一定错误的是( )
| A. | $f({\frac{1}{k}})<\frac{1}{k}$ | B. | $f({\frac{1}{k}})>\frac{1}{k-1}$ | C. | $f({\frac{1}{k-1}})>\frac{1}{k-1}$ | D. | $f({\frac{1}{k-1}})<\frac{1}{k-1}$ |
9.已知椭圆$\frac{x^2}{9}+\frac{y^2}{b^2}=1$(0<b<3),左右焦点分别为F1,F2,过F1的直线交椭圆于A,B两点,若|AF2|+|BF2|的最大值为8,则b的值是( )
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
6.已知向量$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(3,m),若$\overrightarrow{a}$∥(2$\overrightarrow{a}$+$\overrightarrow{b}$),则实数m的值为( )
| A. | -6 | B. | $\frac{3}{2}$ | C. | 6 | D. | $\frac{13}{2}$ |
4.若区间(0,1)上任取一实数b,则方程x2+x+b=0有实根的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |