题目内容
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)记![]() ,试判断函数
,试判断函数![]() 的极值点的情况;
的极值点的情况;
(Ⅱ)若![]() 有且仅有两个整数解,求实数
有且仅有两个整数解,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)
【解析】
(Ⅰ)求导后可知![]() 的符号由
的符号由![]() 的符号决定;根据
的符号决定;根据![]() 的单调性,结合存在性定理可知存在唯一的
的单调性,结合存在性定理可知存在唯一的![]() ,使得
,使得![]() ,从而得到
,从而得到![]() 得单调性,根据极值与单调性的关系可确定极值点;(Ⅱ)将所求不等式化为
得单调性,根据极值与单调性的关系可确定极值点;(Ⅱ)将所求不等式化为![]() ;当
;当![]() 和
和![]() 时,根据(Ⅰ)的结论可验证出都有无穷多个整数解,不合题意;当
时,根据(Ⅰ)的结论可验证出都有无穷多个整数解,不合题意;当![]() 时,若
时,若![]() ,由
,由![]() 时,
时,![]() 可知无整数解,不合题意;若
可知无整数解,不合题意;若![]() ,可知
,可知 ,解不等式组求得结果.
,解不等式组求得结果.
(Ⅰ)由![]() 得:
得:![]()
设![]() ,则
,则![]() 在
在![]() 上单调递增
上单调递增
又![]() ,
,![]()
![]() 存在唯一的
存在唯一的![]() ,使得
,使得![]() ,即
,即![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 上单调递增
上单调递增
![]() 为
为![]() 的极小值点,无极大值点
的极小值点,无极大值点
(Ⅱ)由![]() 得:
得:![]() ,即
,即![]()
①当![]() 时,
时,![]() 恒成立,
恒成立,![]() 有无穷多个整数解,不合题意
有无穷多个整数解,不合题意
②当![]() 时,
时,![]() ,
,![]()
![]() ,
,![]()
![]() 当
当![]() 时,由(Ⅰ)知:
时,由(Ⅰ)知:![]()
![]() 有无穷多个整数解,即
有无穷多个整数解,即![]() 有无穷多个整数解,不合题意
有无穷多个整数解,不合题意
③当![]() 时,
时,![]()
i.当![]() 时,
时,![]() ,又
,又![]()
![]() 两个整数解为:
两个整数解为:![]()
 ,解得:
,解得:
ii.当![]() 时,
时,![]()
当![]() 时,由(Ⅰ)知:
时,由(Ⅰ)知:![]()
![]() 无整数解,不合题意
无整数解,不合题意
综上所述:

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】我市准备实施天然气价格阶梯制,现提前调查市民对天然气价格阶梯制的态度,随机抽查了![]() 名市民,现将调查情况整理成了被调查者的频率分布直方图(如图)和赞成者的频数表如下:
名市民,现将调查情况整理成了被调查者的频率分布直方图(如图)和赞成者的频数表如下:
年龄(岁) |
|
|
|
|
|
|
赞成人数 |
|
|
|
|
|
|
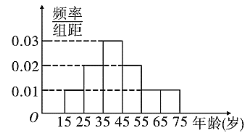
(1)若从年龄在![]() ,
,![]() 的被调查者中各随机选取
的被调查者中各随机选取![]() 人进行调查,求所选取的
人进行调查,求所选取的![]() 人中至少有
人中至少有![]() 人对天然气价格阶梯制持赞成态度的概率;
人对天然气价格阶梯制持赞成态度的概率;
(2)若从年龄在![]() ,
,![]() 的被调查者中各随机选取
的被调查者中各随机选取![]() 人进行调查,记选取的
人进行调查,记选取的![]() 人中对天然气价格实施阶梯制持不赞成态度的人数为
人中对天然气价格实施阶梯制持不赞成态度的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.