题目内容
8．已知对数函数f（x）=（m2-m-1）log（m+1）x，则f（27）=3．分析 利用对数函数的解析式，求出m，然后求解函数值即可．
解答 解：对数函数f（x）=（m2-m-1）log（m+1）x，
可知m2-m-1=1，解得m=2或m=-1，当m=-1时，m+1=0，不满足对数函数的定义，舍去．
对数函数f（x）=log3x，
f（27）=log327=3．
故答案为：3．
点评 本题考查对数函数的定义、解析式的应用，函数值的求法，考查计算能力．
练习册系列答案
相关题目
18．在两个变量y与x的回归模型中，分别选择了四个不同的模型，且它们的R2的值的大小关系为：R${\;}_{模型3}^{2}$＜R${\;}_{模型4}^{2}$＜R${\;}_{模型1}^{2}$＜R${\;}_{模型2}^{2}$，则拟合效果最好的是（ ）
| A． | 模型1 | B． | 模型2 | C． | 模型3 | D． | 模型4 |
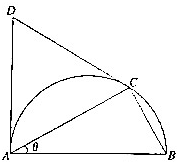如图是一个半径为1的半圆，AB是直径，点C在圆弧上，且与A、B不重合，△ACD是等边三角形，设∠CAB=θ（0＜θ＜$\frac{π}{2}$），