题目内容
设等比数列 的前
的前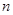 项和为
项和为 ,已知
,已知 成等差数列,(1)求数列
成等差数列,(1)求数列 的公比
的公比 ,(2)若
,(2)若 ,求
,求 ,并讨论
,并讨论 的最大值
的最大值
(1)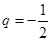 ,(2)
,(2)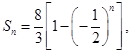
 的最大值为4
的最大值为4
解析试题分析:(1)特殊数列求解方法一般为待定系数法. 因为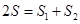 ,以
,以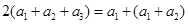 即
即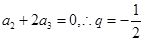 ,此处不用求和公式
,此处不用求和公式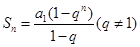 是为了避免讨论
是为了避免讨论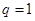 的情况,(2)由(1)已知公比,因此由
的情况,(2)由(1)已知公比,因此由 得
得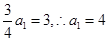
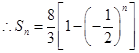 ,当
,当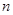 为奇数时
为奇数时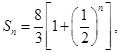 为单调减函数,
为单调减函数,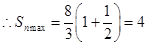 ,当
,当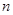 为偶数时
为偶数时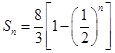 ,为单调增函数,所以
,为单调增函数,所以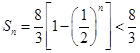 ,由于
,由于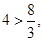 所以
所以 的最大值为4.
的最大值为4.
解 (1)由已知得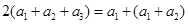 即
即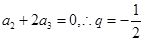 5分
5分
(用求和公式不讨论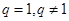 扣2分)
扣2分)
(2)由 得
得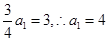
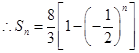 10分
10分
当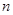 为奇数时
为奇数时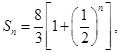
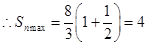 12分
12分
当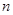 为偶数时
为偶数时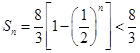 14分
14分
所以 的最大值为4 15分
的最大值为4 15分
考点:等比数列,前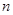 项和最值
项和最值

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
(2011•山东)等比数列{an}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且其中的任何两个数不在下表的同一列.
| | 第一列 | 第二列 | 第三列 |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
(2)若数列{bn}满足:bn=an+(﹣1)nlnan,求数列{bn}的前2n项和S2n.
 ,n∈N*,向量
,n∈N*,向量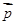 与
与 垂直,且a1=1.
垂直,且a1=1. 中,
中, ,前
,前 项的和是
项的和是 ,且
,且 ,
, .
.
 .
.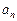 }的前n项和为
}的前n项和为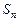 ,且
,且 .
.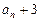 }为等比数列
}为等比数列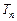
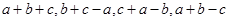 成等比数列, 公比为
成等比数列, 公比为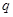 ,求证:
,求证: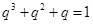 .
.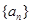 的前
的前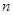 项和为
项和为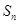 ,且
,且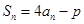 ,其中
,其中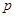 是不为零的常数.
是不为零的常数.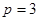 时,数列
时,数列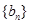 满足
满足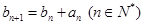 ,
,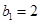 ,求数列
,求数列