题目内容
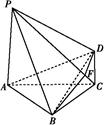
如图,四棱锥P-ABCD的底面是矩形,侧面PAD丄底面ABCD,. .
.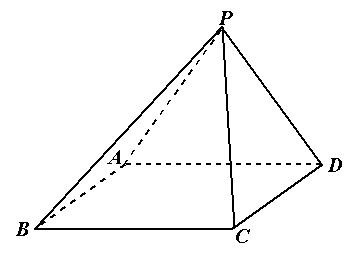
(1)求证:平面PAB丄平面PCD
(2)如果AB=BC=2,PB=PC=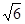 求四棱锥P-ABCD的体积.
求四棱锥P-ABCD的体积.
(1) 见解析 (2)
解析试题分析:(1)欲证平面 平面
平面 ,只需证其中的一个平面经过另一平面的一条垂线即可,考虑到题设中所给的矩形以及面面垂直关系,易证:
,只需证其中的一个平面经过另一平面的一条垂线即可,考虑到题设中所给的矩形以及面面垂直关系,易证: ,从而
,从而 平面
平面 ;
;
(2)作 ,垂足为
,垂足为 ,连结
,连结 ;可证
;可证 ≌
≌



 是
是 的中点,
的中点,
从而求得四棱锥的高 ,进一步求得四棱锥
,进一步求得四棱锥 的体积.
的体积.
试题解析:(Ⅰ)因为四棱锥 的底面是矩形,所以
的底面是矩形,所以 ,
,
又侧面 底面
底面 ,所以
,所以 .
.
又 ,即
,即 ,而
,而 ,所以
,所以 平面
平面 .
.
因为PAÌ平面PAB,所以平面PAB⊥平面PCD. 4分
(Ⅱ)如图,作PO⊥AD,垂足为O,则PO⊥平面ABCD.
连结OB,OC,则PO⊥OB,PO⊥OC.
因为PB=PC,所以Rt△POB≌Rt△POC,所以OB=OC.
依题意,ABCD是边长为2的正方形,由此知O是AD的中点. 7分
在Rt△OAB中,AB=2,OA=1,OB= .
.
在Rt△OAB中,PB= ,OB=
,OB= ,PO=1. 10分
,PO=1. 10分
故四棱锥P-ABCD的体积V= AB2·PO=
AB2·PO= .
.
考点:1、平面与平面垂直的判定与性质;2、棱锥的体积.

练习册系列答案
相关题目
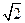 ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.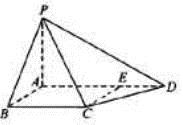
 的边长为3,
的边长为3, 与
与 交于
交于 ,且
,且 .将菱形
.将菱形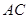 折起得到三棱锥
折起得到三棱锥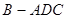 (如图),点
(如图),点 是棱
是棱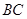 的中点,
的中点, .
.

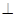 平面
平面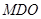 ;
;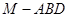 的体积.
的体积. 与
与 都是边长为
都是边长为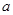 的正方形,点
的正方形,点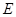 是
是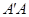 的中点,
的中点,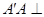 平面
平面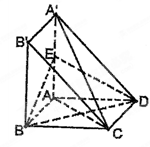
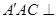 平面
平面 ;
; 的体积.
的体积.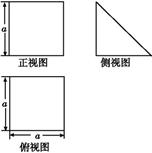

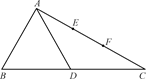

 ABCD中,PA⊥底面ABCD,PA=2
ABCD中,PA⊥底面ABCD,PA=2 ,BC="CD=2," ∠ACB=∠ACD=
,BC="CD=2," ∠ACB=∠ACD=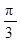 .
.
 A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=
A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=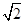 .
.