题目内容
19.${∫}_{1}^{2}$2xdx=3.分析 由题意可得${∫}_{1}^{2}$2xdx=x2${|}_{1}^{2}$,代值计算可得.
解答 解:由定积分的计算可得:
${∫}_{1}^{2}$2xdx=x2${|}_{1}^{2}$=22-12=3
故答案为:3
点评 本题考查定积分的计算,属基础题.

练习册系列答案
相关题目
9.函数$f(x)={log_3}(-{x^2}+2x)$的单调递减区间为( )
| A. | (1,+∞) | B. | (1,2) | C. | (0,1) | D. | (-∞,1) |
7.已知$a={log_{\frac{1}{5}}}\frac{1}{3},b={log_5}\frac{1}{3},c={(\frac{1}{5})^{\frac{1}{2}}}$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>b>a |
11.已知函数f(x)=cos2x-sin2x,下列结论中错误的是( )
| A. | f(x)=cos2x | B. | f(x)的最小正周期为π | ||
| C. | f(x)的图象关于直线x=0对称 | D. | f(x)的值域为[-$\sqrt{2}$,$\sqrt{2}$] |
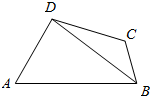 如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.
如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.