题目内容
1.若不等式ax2-bx+c>0的解集是(-1,2),则有以下结论:①a>0,②b<0且c>0,③a+b+c<0,④a-b+c>0,⑤不等式ax2+bx+c>0的解集是(-2,1).其中正确结论的序号是②.分析 根据“不等式ax2-bx+c>0的解集是(-1,2),”可判断a<0,-1,2,是ax2+bx+c=0的二根,从而可判断b,c的符号,问题即可解决.
解答 解:由题意可知:a<0,①错误,
-1,2是ax2-bx+c=0的二根,∴-1+2=1=$\frac{b}{a}$,-1×2=$\frac{c}{a}$,∴b=a,c=-2a,∴b<0,c>0,∴②正确,
令f(x)=ax2-bx+c,由题意可知f(1)=a+b+c>0,∴③错误,
f(-1)=a+b+c=0,∴④错误,
∵ax2+bx+c=0,设其两根为x1,x2,
∴x1+x2=-$\frac{b}{a}$=-1,x1•x2=$\frac{c}{a}$=-2,
∴不等式ax2+bx+c>0的解集是(-2,-1),∴⑤错误,
故答案为:②
点评 本题考查一元二次不等式的应用,着重考查三个“二次”(二次函数y=ax2+bx+c(a≠0),一元二次不等式,一元二次方程ax2+bx+c=0(a≠0)))之间的关系,属于中档题.

练习册系列答案
相关题目
12.阅读以下程序:

若输出y=16,则输入的x值应该是( )

若输出y=16,则输入的x值应该是( )
| A. | 3或-3 | B. | -5或5 | C. | 5或-3 | D. | -5 |
9.等差数列{an}的前n项和为Sn,已知a1=-12,S13=0,使得an>0的最小正整数n等于( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
16.5人站成一排,甲乙之间恰有一个人的站法有( )
| A. | 18 | B. | 24 | C. | 36 | D. | 48 |
 (
( 为常数,
为常数,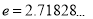 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点 处的切线与
处的切线与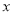 轴平行.
轴平行.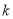 的值;
的值; 的单调区间;
的单调区间; ,其中
,其中 为
为 的导函数.证明:对任意
的导函数.证明:对任意 ,
,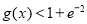 .
. 为偶函数,则
为偶函数,则 .
.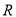 的函数
的函数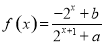 是奇函数.
是奇函数.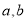 的值;
的值;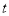 的不等式
的不等式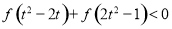 .
.