题目内容
已知a>0,b>0,a+b=4,求(a+
解:∵a+b=4,∴a2+b2=(a+b)2-2ab=16-2ab. 又a2+b2≥2ab,∴16-2ab≥2ab,即ab≤4. ∴(a+ 故(a+
![]() )2+(b+
)2+(b+![]() )2≥
)2≥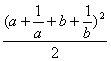 =
=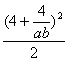 =
=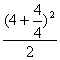 =
=![]() .
.![]() )2+(b+
)2+(b+![]() )2的最小值是
)2的最小值是![]() .
. 练习册系列答案
练习册系列答案

开心夺冠系列答案
同步测控全优设计系列答案
领航新课标练习册系列答案
培优大考卷系列答案
全程闯关100分系列答案
自主预习与评价系列答案

佳分卷系列答案
考点全易通系列答案
相关题目
 的夹角是( )
的夹角是( ) C.
C. D.
D.