题目内容
已知,tan(
+α)=3,计算:
(1)tanα
(2)
(3)sinα•cosα
| π |
| 4 |
(1)tanα
(2)
| 2sinαcosα+3cos2α |
| 5cos2α-3sin2α |
(3)sinα•cosα
(1)∵已知tan(
+α)=3=
,∴tanα=
.
(2)由(1)可得tan2α=
=
=
.
=
=
=
=
.
(3)sinα•cosα=
=
=
=
.
| π |
| 4 |
| 1+tanα |
| 1-tanα |
| 1 |
| 2 |
(2)由(1)可得tan2α=
| 2tanα |
| 1-tan2α |
| 1 | ||
1-
|
| 4 |
| 3 |
| 2sinαcosα+3cos2α |
| 5cos2α-3sin2α |
| sin2α+3cos2α |
| 5cos2α-3sin2α |
| tan2α+3 |
| 5-3tan2α |
| ||
5-3×
|
| 13 |
| 3 |
(3)sinα•cosα=
| sinαcosα |
| cos2α+sin2α |
| tanα |
| 1+tan2α |
| ||
1+
|
| 2 |
| 5 |

练习册系列答案
相关题目
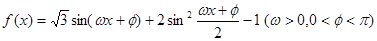 为奇函数,且相邻两对称轴间的距离为
为奇函数,且相邻两对称轴间的距离为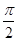 .
.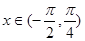 时,求
时,求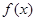 的单调递减区间;
的单调递减区间; 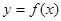 的图象沿
的图象沿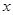 轴方向向右平移
轴方向向右平移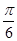 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的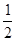 (纵坐标不变),得到函数
(纵坐标不变),得到函数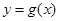 的图象.当
的图象.当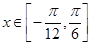 时,求函数
时,求函数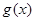 的值域.
的值域. ,
, ,求
,求 的值.
的值.