Question

求下列函数的定义域：

(1)y=2-sinx;

(2)y=lg(cosx);

(3)y=.

Answer 1

解析:(1)∵sinx有意义，则x∈R,

∴y=2-sinx的定义域为R.

(2)要使函数有意义，则cosx＞0,可知

2kπ-＜x＜2kπ+,k∈Z.

∴y=lg(cosx)的定义域为(2kπ-,2kπ+)(k∈Z).

(3)要使函数有意义，则应满足：

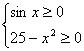
(k∈Z).

由图可得-5≤x≤-π或0≤x≤π.

∴y=的定义域为［-5，-π］∪［0，π］.

点评：正弦函数y=sinx和余弦函数y=cosx的定义域均为R，但在求由它们与其他函数复合而成的函数定义域时，先由解析式有意义得到关于正弦和余弦的三角不等式组再解之即可.