题目内容
设函数f（x）=3sinx+2cosx+1．若实数a、b、c使得af（x）+bf（x-c）=1对任意实数x恒成立，则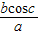
的值等于（ ）A．
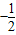
B．
C．-1
D．1
【答案】分析：作为一个选择题，可以令c取特殊值π来求解，找出一个符合af（x）+bf（x-c）=1对任意实数x恒成立的a、b、c，代入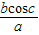
可求出所求．
解答：解：令c=π，则对任意的x∈R，都有f（x）+f（x-π）=3sinx+2cosx+1+3sin（x-π）+2cos（x-π）+1=2，
于是取a=b=
，c=π，则对任意的x∈R，af（x）+bf（x-c）=1，由此得
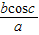=-1．
故选C．
点评：本题主要考查了函数恒成立问题，以及赋值法的应用，同时考查了运算求解的能力，属于中档题．
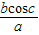可求出所求．解答：解：令c=π，则对任意的x∈R，都有f（x）+f（x-π）=3sinx+2cosx+1+3sin（x-π）+2cos（x-π）+1=2，
于是取a=b=
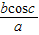，c=π，则对任意的x∈R，af（x）+bf（x-c）=1，由此得=-1．故选C．
点评：本题主要考查了函数恒成立问题，以及赋值法的应用，同时考查了运算求解的能力，属于中档题．
练习册系列答案
小学能力测试卷系列答案
相关题目