题目内容
椭圆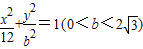
与渐近线为x±2y=0的双曲线有相同的焦点F1，F2，P为它们的一个公共点，且∠F1PF2=90°，则椭圆的离心率为（ ）A．
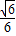
B．
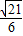
C．
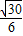
D．
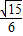
【答案】分析：由渐近线为x±2y=0，得出双曲线中的实轴长与半焦距的关系a2=
，再结合椭圆和双曲线的定义，列出关于PF1，PF2，F1F2的关系式，解出c的值，代入离心率公式计算．
解答：解：设F1F2=2c，在双曲线中，
=
，a2+b2=c2，得a2=
．不妨设p在第一象限，则由椭圆的定义得PF1+PF2=
，由双曲线的定义得PF1-PF2=2a=
又∠F1PF2=90°∴PF12+PF22=4c2∴48+
=8c2，解c=
，∴e=
=
=
．
故选C
点评：本题是椭圆和双曲线结合的好题．要充分认识到PF1，PF2，F1F2在两曲线中的沟通作用．
，再结合椭圆和双曲线的定义，列出关于PF1，PF2，F1F2的关系式，解出c的值，代入离心率公式计算．解答：解：设F1F2=2c，在双曲线中，
=，a2+b2=c2，得a2=．不妨设p在第一象限，则由椭圆的定义得PF1+PF2=，由双曲线的定义得PF1-PF2=2a=又∠F1PF2=90°∴PF12+PF22=4c2∴48+=8c2，解c=，∴e===．故选C
点评：本题是椭圆和双曲线结合的好题．要充分认识到PF1，PF2，F1F2在两曲线中的沟通作用．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
与渐近线为x±2y=0的双曲线有相同的焦点F1，F2，P为它们的一个公共点，且∠F1PF2=90°，则椭圆的离心率为
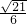
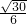
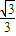x，且它的一条准线与渐近线y=
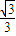x及x轴围成的三角形的周长是
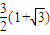．以C1的两个顶点为焦点，以C1的焦点为顶点的椭圆记为C2．
的直线l经过定点P（m，0）（m＞0）并与椭圆C2交于不同的两点A、B，若对于椭圆C2上任意一点M，都存在θ∈[0，2π]，使得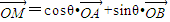
成立．求实数m的值．