题目内容
1.设函数y=f(x)=loga(a-kax)(a>0,a≠1,k∈R)(1)若函数y=f(x)的反函数就是其本身,求k的值;
(2)在(1)的条件下,求f(x)≥1的解集;
(3)我们学过许多函数的反函数就是其本身.例如y=x,y=$\frac{1}{x}$等,请你再举出除了上述3种类型之外的2个函数,使得函数的反函数就是其本身.
分析 (1)求出y=f(x)的反函数,根据f(x)的原函数与反函数相同,列出方程,求出k的值;
(2)k=1时,由f(x)≥1得出为loga(a-ax)≥1,讨论a的取值范围,求出不等式的解集;
(3)举例说明函数的反函数是其本身的函数即可.
解答 解:(1)∵y=f(x)=loga(a-kax),
∴ay=a-kax,
∴x=loga$\frac{a{-a}^{y}}{k}$,
∴f(x)的反函数为y=loga$\frac{a{-a}^{x}}{k}$;
又∵f(x)的原函数与反函数是同一函数,
∴loga(a-kax)=loga$\frac{a{-a}^{x}}{k}$恒成立,
即a-kax=$\frac{a{-a}^{x}}{k}$恒成立,
即(k2-1)ax+(1-k)a=0恒成立,
∴$\left\{\begin{array}{l}{{k}^{2}-1=0}\\{1-k=0}\end{array}\right.$,
解得k=1;
(2)k=1时,f(x)=loga(a-ax),
不等式f(x)≥1即为loga(a-ax)≥1;
当a>1时,不等式化为a-ax≥a,即ax≤0,无解;
当1>a>0时,不等式化为0<a-ax≤a,即a>ax≥0,解得x>1;
综上,a>1时,不等式无解,
1>a>0时,不等式的解集为{x|x>1};
(3)函数的反函数是其本身的函数有y=-$\frac{1}{x}$(x≠0)与y=-x等.
点评 本题考查了分类讨论的应用问题,也考查了对数函数函数与反函数的应用问题,考查了不等式的解法与应用问题,是综合性题目.

练习册系列答案
相关题目
11.已知曲线C1:$\frac{{x}^{2}}{3}$+y2=1和C2:x2-y2=1,且曲线Cl的焦点分别为F1、F2,点M是C1和C2的一个交点,则△MF1F2的形状是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 都有可能 |
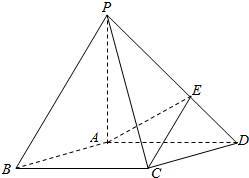 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E是PD的中点.
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E是PD的中点.