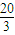Question

从边长为10 cm×16 cm的矩形纸板的四个角，截去四个相同的小正方形，做成一个无盖的盒子，盒子的最大容积为______cm³（　　）

• A、2
• B、

  20

  3

• C、144
• D、

  1600

  27

Answer 1

分析：设截去四个相同的小正方形的边长为x，列出体积表达式，通过求导求出最大值．

解答：解：设截去四个相同的小正方形的边长为x，则盒子的容积
为：V=（10-2x）（16-2x）x=4x（5-x）（8-x）
V=4（40x-13x²+4^3）
∴V′=4（40-26x+3x²）
令V′=0即：40-26x+3x²=0
解得x=2或x=

20

3

舍去，
当x=2时盒子的最大容积为：144
故答案为：144

点评：本题考查长方体的体积的最大值问题，考查形式求导法则的应用，考查计算能力，是中档题．