题目内容
已知
（n∈N*）（Ⅰ）求f（1），f（2），f（3），f（4）归纳并猜想f（n）
（Ⅱ）用数学归纳证明你的猜想．
【答案】分析：（I）分别计算f（1）=
，f（2）=1-
=
，f（3），f（4），归纳并猜想f（n）=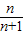
；
（II）用数学归纳法证明，①检验n=1时，猜想成立；②假设当n=k时，命题成立，即f（k）=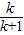
，再证明当n=k+1时，也成立，从而猜想成立．
解答：解：（I）分别计算f（1）=
，
f（2）=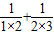
=1-
=
，
f（3）=1-
=
，
f（4）=1-
=
，
归纳并猜想f（n）=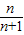
（n∈N*）；
（II）证明：①当n=1 时，由上面计算知结论正确．
②假设n=k时等式成立，即f（k）=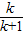
，
则当n=k+1时，f（k+1）=f（k）+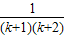
=
+
=
，
即n=k+1时等式成立．
由①②知，等式对任意正整数都成立．
点评：本题考查根据递推关系求数列的通项公式的方法，考查数学归纳法，证明n=k+1时，是解题的难点．
，f（2）=1-=，f（3），f（4），归纳并猜想f（n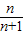）=；（II）用数学归纳法证明，①检验n=1时，猜想成立；②假设当n=k时，命题成立，即f（k）=
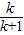，再证明当n=k+1时，也成立，从而猜想成立．解答：解：（I）分别计算f（1）=
，f（2）=
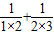=1-=，f（3）=1-
=，f（4）=1-
=，归纳并猜想f（n）=
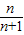（n∈N*）；（II）证明：①当n=1 时，由上面计算知结论正确．
②假设n=k时等式成立，即f（k）=
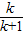，则当n=k+1时，f（k+1）=f（k）+
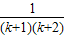=+=，即n=k+1时等式成立．
由①②知，等式对任意正整数都成立．
点评：本题考查根据递推关系求数列的通项公式的方法，考查数学归纳法，证明n=k+1时，是解题的难点．
练习册系列答案
考前必练系列答案
相关题目
已知n∈N*，则不等式|
-2|＜0.01的解集为（ ）
| 2n |
| n+1 |
| A、{n|n≥199，n∈N*} |
| B、{n|n≥200，n∈N*} |
| C、{n|n≥201，n∈N*} |
| D、{n|n≥202，n∈N*} |
